题目内容
11.下列命题中,其逆命题成立的是( )①同旁内角互补,两直线平行;
②如果两个角是直角,那么它们相等;
③如果两个实数相等,那么它们的平方相等;
④如果三角形的三边长a,b,c,满足a2+b2=c2,那么这个三角形是直角三角形.
| A. | ①④ | B. | ①②④ | C. | ②③ | D. | ①③ |
分析 把一个命题的条件和结论互换就得到它的逆命题,再把逆命题进行判断即可.
解答 解:①同旁内角互补,两直线平行的逆命题是两直线平行,同旁内角互补,成立;
②如果两个角是直角,那么它们相等的逆命题是如果两个角相等,那么这两个角是直角,不成立;
③如果两个实数相等,那么它们的平方相等的逆命题是如果两个数的平方相等,那么这两个数相等,不成立;
④如果一个三角形是直角三角形,c为斜边,则a2+b2=c2,正确.
逆命题成立的有①④个;
故选A.
点评 此题考查了命题与定理,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题,其中一个命题称为另一个命题的逆命题,解体的关键是熟练掌握课本上的定理.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
19.已知(1,y1),(-3,y2),(-4,y3)是抛物线y=-2x2-8x+m上的点,则( )
| A. | y1<y2<y3 | B. | y2>y1>y3 | C. | y3<y2<y1 | D. | y2>y3>y1 |
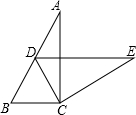 如图,在Rt△ABC中,∠ACB=90°,∠A=24°,将△ABC绕点C按顺时针方向旋转后得到△EDC,此时点D在AB边上,旋转角为48°.
如图,在Rt△ABC中,∠ACB=90°,∠A=24°,将△ABC绕点C按顺时针方向旋转后得到△EDC,此时点D在AB边上,旋转角为48°.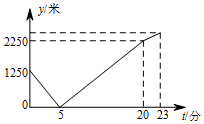 早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的图象如图所示,根据题意填空:
早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的图象如图所示,根据题意填空: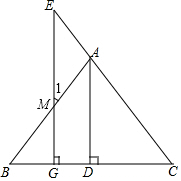 如图,若AD⊥BC,EG⊥BC,∠1=∠E,则AD为∠BAC的平分线,请你说明理由.
如图,若AD⊥BC,EG⊥BC,∠1=∠E,则AD为∠BAC的平分线,请你说明理由.