题目内容
20.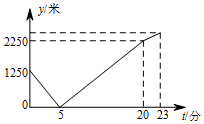 早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的图象如图所示,根据题意填空:
早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的图象如图所示,根据题意填空:①打电话时,小刚和妈妈的距离为1250米;
②打完电话后,经过23分钟小刚到达学校;
③小刚和妈妈相遇后,妈妈回家的速度为50米/分;
④小刚家与学校的距离为2550米.
分析 ①根据函数图象可以直接得到打电话时,小刚和妈妈的距离;
②根据函数图象可以得到打完电话后,经过多少分钟小刚到达学校;
③根据题意和函数图象中的数据可以求得小刚和妈妈相遇后,妈妈回家的速度;
④根据题意和图象中的数据可以求得小刚家与学校的距离.
解答 解:①由图象可得,
打电话时,小刚和妈妈的距离为:1250米,
故答案为:1250;
②由图象可得,
打完电话后,经过23分钟小刚到达学校,
故答案为:23;
③由题意可得,
小刚和妈妈相遇后,妈妈回家的速度为:(1250-5×100)÷15=50米/分,
故答案为:50;
④由题意可得,
小刚家与学校的距离为:
(1250-5×100)+(23-5)×100
=(1250-500)+18×100
=750+1800
=2550(米),
故答案为:2550.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
相关题目
11.下列命题中,其逆命题成立的是( )
①同旁内角互补,两直线平行;
②如果两个角是直角,那么它们相等;
③如果两个实数相等,那么它们的平方相等;
④如果三角形的三边长a,b,c,满足a2+b2=c2,那么这个三角形是直角三角形.
①同旁内角互补,两直线平行;
②如果两个角是直角,那么它们相等;
③如果两个实数相等,那么它们的平方相等;
④如果三角形的三边长a,b,c,满足a2+b2=c2,那么这个三角形是直角三角形.
| A. | ①④ | B. | ①②④ | C. | ②③ | D. | ①③ |
8.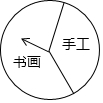 某班“红领巾义卖”活动中设立了一个可以自由转动的转盘.规定:顾客购物20元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
某班“红领巾义卖”活动中设立了一个可以自由转动的转盘.规定:顾客购物20元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
(1)完成上述表格:a=295;b=0.745;
(2)请估计当n很大时,频率将会接近0.6,假如你去转动该转盘一次,你获得“书画作品”的概率约是0.6;(结果全部精确到0.1)
(3)如果要使获得“手工作品”的可能性大于获得“书画作品”的可能性,则表示“手工作品”区域的扇形的圆心角至少还要增加是多少度?
 某班“红领巾义卖”活动中设立了一个可以自由转动的转盘.规定:顾客购物20元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
某班“红领巾义卖”活动中设立了一个可以自由转动的转盘.规定:顾客购物20元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:| 转动转盘的次数n | 100 | 200 | 300 | 400 | 500 | 1000 |
| 落在“书画作品”区域的次数m | 60 | 122 | 180 | 298 | a | 604 |
| 落在“书画作品”区域的频率$\frac{m}{n}$ | 0.6 | 0.61 | 0.6 | b | 0.59 | 0.604 |
(2)请估计当n很大时,频率将会接近0.6,假如你去转动该转盘一次,你获得“书画作品”的概率约是0.6;(结果全部精确到0.1)
(3)如果要使获得“手工作品”的可能性大于获得“书画作品”的可能性,则表示“手工作品”区域的扇形的圆心角至少还要增加是多少度?
9.下列二次根式中,是最简二次根式的是( )
| A. | $\sqrt{4}$ | B. | $\sqrt{\frac{1}{5}}$ | C. | $\sqrt{10}$ | D. | $\sqrt{0.5}$ |

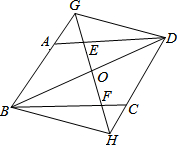 如图,在平行四边形ABCD中,AB=3,BC=4,∠ABC=60°,过对角线BD的中点O的直线GH分别交AD、BC于点E、F,交BA的延长线于点G,交DC的延长线于点H,连结GD、BH,则下列结论:①AG=CH,②DE+CF=5,③S四边形ABFE=3$\sqrt{3}$,④四边形BGDH为平行四边形.其中正确的有( )
如图,在平行四边形ABCD中,AB=3,BC=4,∠ABC=60°,过对角线BD的中点O的直线GH分别交AD、BC于点E、F,交BA的延长线于点G,交DC的延长线于点H,连结GD、BH,则下列结论:①AG=CH,②DE+CF=5,③S四边形ABFE=3$\sqrt{3}$,④四边形BGDH为平行四边形.其中正确的有( )