题目内容
3．
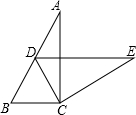如图，在Rt△ABC中，∠ACB=90°，∠A=24°，将△ABC绕点C按顺时针方向旋转后得到△EDC，此时点D在AB边上，旋转角为48°．
分析 根据直角三角形两锐角互余求出∠B，再根据旋转的性质可得BC=CD，然后根据等腰三角形两底角相等求出∠BCD，然后根据对应边BC、CD的夹角即为旋转角解答．
解答 解：∵∠ACB=90°，∠A=24°，
∴∠B=90°-24°=66°，
∵△ABC绕点C按顺时针方向旋转后得到△EDC，点D在AB边上，
∴BC=CD，
∠BCD=180°-66°×2=48°，
∴旋转角为48°．
故答案为：48．
点评 本题考查了旋转的性质，等腰三角形的性质，直角三角形两锐角互余的性质，熟记各性质是解题的关键．
练习册系列答案
相关题目
用10米长的铝合金做成一个长方形的窗框（如图），设长方形窗框的横条长度为x米，则长方形窗框的面积为x（5-1.5x）平方米．
11．下列命题中，其逆命题成立的是（ ）
①同旁内角互补，两直线平行；
②如果两个角是直角，那么它们相等；
③如果两个实数相等，那么它们的平方相等；
④如果三角形的三边长a，b，c，满足a2+b2=c2，那么这个三角形是直角三角形．
①同旁内角互补，两直线平行；
②如果两个角是直角，那么它们相等；
③如果两个实数相等，那么它们的平方相等；
④如果三角形的三边长a，b，c，满足a2+b2=c2，那么这个三角形是直角三角形．
| A． | ①④ | B． | ①②④ | C． | ②③ | D． | ①③ |
8．
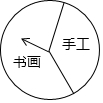某班“红领巾义卖”活动中设立了一个可以自由转动的转盘．规定：顾客购物20元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品．下表是此次活动中的一组统计数据：
（1）完成上述表格：a=295；b=0.745；
（2）请估计当n很大时，频率将会接近0.6，假如你去转动该转盘一次，你获得“书画作品”的概率约是0.6；（结果全部精确到0.1）
（3）如果要使获得“手工作品”的可能性大于获得“书画作品”的可能性，则表示“手工作品”区域的扇形的圆心角至少还要增加是多少度？
某班“红领巾义卖”活动中设立了一个可以自由转动的转盘．规定：顾客购物20元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品．下表是此次活动中的一组统计数据：| 转动转盘的次数n | 100 | 200 | 300 | 400 | 500 | 1000 |
| 落在“书画作品”区域的次数m | 60 | 122 | 180 | 298 | a | 604 |
| 落在“书画作品”区域的频率$\frac{m}{n}$ | 0.6 | 0.61 | 0.6 | b | 0.59 | 0.604 |
（2）请估计当n很大时，频率将会接近0.6，假如你去转动该转盘一次，你获得“书画作品”的概率约是0.6；（结果全部精确到0.1）
（3）如果要使获得“手工作品”的可能性大于获得“书画作品”的可能性，则表示“手工作品”区域的扇形的圆心角至少还要增加是多少度？
