题目内容
2.化简$\root{4}{7+4\sqrt{3}}$+$\root{4}{7-4\sqrt{3}}$.分析 原式利用二次根式性质,以及分数指数幂法则计算即可得到结果.
解答 解:原式=$\root{4}{(2+\sqrt{3})^{2}}$+$\root{4}{(2-\sqrt{3})^{2}}$
=$\sqrt{2+\sqrt{3}}$+$\sqrt{2-\sqrt{3}}$
=$\sqrt{\frac{1}{2}(\sqrt{3}+1)^{2}}$+$\sqrt{\frac{1}{2}(\sqrt{3}-1)^{2}}$
=($\sqrt{3}$+1)•$\frac{\sqrt{2}}{2}$+($\sqrt{3}$-1)•$\frac{\sqrt{2}}{2}$
=2$\sqrt{3}$×$\frac{\sqrt{2}}{2}$
=$\sqrt{6}$.
点评 此题考查了实数的运算,以及分数指数幂,熟练掌握运算法则是解本题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
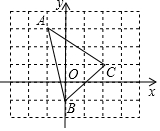 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,3),B(0,-1),C(2,1).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,3),B(0,-1),C(2,1).


