题目内容
10.定义新运算:对于任意不为零的实数a、b,都有a★b=$\frac{1}{a}$-$\frac{1}{b}$,求方程x★(2-x)=$\frac{6}{{x}^{2}-2x}$的解.分析 根据a★b=$\frac{1}{a}$-$\frac{1}{b}$,可得:x★(2-x)=$\frac{1}{x}$-$\frac{1}{2-x}$=$\frac{6}{{x}^{2}-2x}$,据此求出方程的解即可.
解答 解:∵a★b=$\frac{1}{a}$-$\frac{1}{b}$,
∴x★(2-x)=$\frac{1}{x}$-$\frac{1}{2-x}$=$\frac{6}{{x}^{2}-2x}$,
两边同时乘x(2-x),可得:2-x-x=-6,
解得x=4,
经检验,x=4是原分式方程的解,
∴原分式方程的解为:x=4.
点评 此题主要考查了实数的运算,以及分式方程的求解方法,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.

练习册系列答案
相关题目
14. 如图,从位置P到直线公路MN共有四条小道,若用相同的速度行走,能最快到达公路MN的小道是( )
如图,从位置P到直线公路MN共有四条小道,若用相同的速度行走,能最快到达公路MN的小道是( )
 如图,从位置P到直线公路MN共有四条小道,若用相同的速度行走,能最快到达公路MN的小道是( )
如图,从位置P到直线公路MN共有四条小道,若用相同的速度行走,能最快到达公路MN的小道是( )| A. | PA | B. | PB | C. | PC | D. | PD |
1.下列长度的3条线段不能构成直角三角形的是( )
| A. | 8,15,17 | B. | 12,16,20 | C. | 5,12,13 | D. | 7,8,10 |
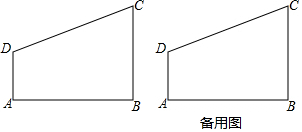 已知,直角梯形ABCD中,∠B=90°,AD=1,BC=2,AB=3,点M位于线段AB上,且△DMC是直角三角形,求线段AM的长度.
已知,直角梯形ABCD中,∠B=90°,AD=1,BC=2,AB=3,点M位于线段AB上,且△DMC是直角三角形,求线段AM的长度.