题目内容
2.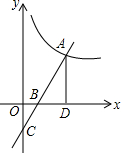 如图,直线y=2x-4与反比例函数y=$\frac{k}{x}$的图象交于第一象限的点A,与x轴、y轴分别交于点B,C,AD⊥x轴于点D.如果△BOC与△BDA的面积之比等于4:9,则k=30.
如图,直线y=2x-4与反比例函数y=$\frac{k}{x}$的图象交于第一象限的点A,与x轴、y轴分别交于点B,C,AD⊥x轴于点D.如果△BOC与△BDA的面积之比等于4:9,则k=30.
分析 由已知两三角形相似,利用面积比等于相似比的平方求出相似比为2:3,可得出OB与BD之比为2:3,由直线与x轴的交点坐标求出OB的长,确定出BD的长,由OB+BD求出OD的长,即为A的横坐标,代入直线方程求出A的纵坐标,确定出A的坐标,将A坐标代入反比例解析式中求出k的值,即可确定出反比例解析式.
解答 解:∵AD⊥x轴于点D,
∴AD∥y轴,
∴△OBC∽△DBA,
∵△BOC与△BDA的面积之比等于4:9,
∴OB:BD=2:3,
对于直线y=2x-4,令y=0求出x=2,即OB=2,
∴BD=3,OD=OB+BD=5,
将x=5代入直线方程y=2x-4中,得:y=6,
∴A(5,6),
将A坐标代入反比例解析式得:k=30;
故答案为30.
点评 此题考查了反比例函数与一次函数的交点问题,涉及的知识有:相似三角形的判定与性质,一次函数与x轴的交点,以及待定系数法求反比例解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
12.已知实数a,b,若a>b,则下列结论正确的是( )
| A. | a-2<b-2 | B. | 2+a<2+b | C. | $\frac{a}{2}$<$\frac{b}{2}$ | D. | -2a<-2b |
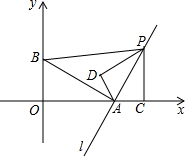 如图,在直角坐标系中,点A(4,0),点B(0,2),过点A的直线l⊥线段AB,P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处,且以点A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标是P(5,2),P(8,8),P(0,-8),P(3,-2).
如图,在直角坐标系中,点A(4,0),点B(0,2),过点A的直线l⊥线段AB,P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处,且以点A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标是P(5,2),P(8,8),P(0,-8),P(3,-2).