题目内容
18.如图,数轴上有A、B、C、D四点,根据图中各点的位置,判断那一点所表示的数与4-2$\sqrt{6}$最接近?( )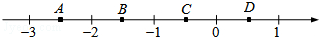
| A. | A | B. | B | C. | C | D. | D |
分析 先确定2$\sqrt{6}$的范围,再求出4-2$\sqrt{6}$的范围,根据数轴上点的位置得出即可.
解答 解:∵$\sqrt{16}$<2$\sqrt{6}$=$\sqrt{24}$<$\sqrt{25}$,
∴4<2$\sqrt{6}$<5,
∴-5<-2$\sqrt{6}$<-4,
∴-1<4-2$\sqrt{6}$<0,
故选:C.
点评 本题考查了数轴和估算无理数的大小的应用,解此题的关键是求出4-2$\sqrt{6}$的范围.

练习册系列答案
相关题目
8.下列计算不正确的是( )
| A. | (-2)-2=-$\frac{1}{4}$ | B. | ($\frac{1}{3}$)-2=9 | ||
| C. | 20050=20080 | D. | 3.2×10-4=0.00032. |
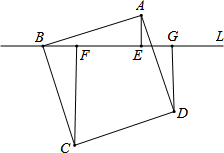 如图,过正方形ABCD的顶点B作直线L,过A,C,D作L的垂线.垂足分别为点E,F,G.若AE=2,CF=6,则CF+AE+DG的值为12.
如图,过正方形ABCD的顶点B作直线L,过A,C,D作L的垂线.垂足分别为点E,F,G.若AE=2,CF=6,则CF+AE+DG的值为12.
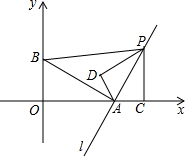 如图,在直角坐标系中,点A(4,0),点B(0,2),过点A的直线l⊥线段AB,P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处,且以点A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标是P(5,2),P(8,8),P(0,-8),P(3,-2).
如图,在直角坐标系中,点A(4,0),点B(0,2),过点A的直线l⊥线段AB,P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处,且以点A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标是P(5,2),P(8,8),P(0,-8),P(3,-2).