题目内容
15.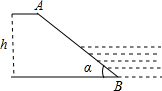 如图所示,一水库迎水坡AB的坡度i=1:2,则求坡角α的正弦值sinα=$\frac{\sqrt{5}}{5}$.
如图所示,一水库迎水坡AB的坡度i=1:2,则求坡角α的正弦值sinα=$\frac{\sqrt{5}}{5}$.
分析 过A作AC⊥BC于C,根据坡角和坡度的概念,得tanα=$\frac{AC}{BC}$=$\frac{1}{2}$,设AC=x,BC=2x,根据勾股定理求出AB的长,即可求出sinα的值.
解答 解:过A作AC⊥BC于C,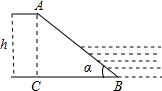
∵AB的坡度i=1:3,
∴tanα=$\frac{AC}{BC}$=$\frac{1}{2}$,
设AC=x,BC=3x,
根据勾股定理可得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{5}$x,
则sinα=$\frac{AC}{AB}$=$\frac{x}{\sqrt{5}x}$=$\frac{\sqrt{5}}{5}$.
故答案为:$\frac{\sqrt{5}}{5}$.
点评 本题考查了坡度坡角的知识,属于基础题,解答本题的关键是熟练掌握勾股定理的应用及坡角的定义.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.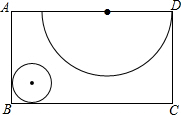 如图,矩形ABCD纸板中,剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若已知小圆的半径为1cm,则此圆锥的全面积是( )
如图,矩形ABCD纸板中,剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若已知小圆的半径为1cm,则此圆锥的全面积是( )
 如图,矩形ABCD纸板中,剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若已知小圆的半径为1cm,则此圆锥的全面积是( )
如图,矩形ABCD纸板中,剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若已知小圆的半径为1cm,则此圆锥的全面积是( )| A. | 2πcm | B. | 3πcm | C. | $\sqrt{3}$πcm | D. | ($\sqrt{3}$+1)πcm |
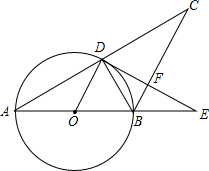 如图,在△ABC中,AB=BC,以AB为直径的圆O交BC于点D,过点D作DF⊥BC,交AB的延长线于E,垂足为F.若∠A=30°,BC=6,则DF=$\frac{3\sqrt{3}}{2}$.
如图,在△ABC中,AB=BC,以AB为直径的圆O交BC于点D,过点D作DF⊥BC,交AB的延长线于E,垂足为F.若∠A=30°,BC=6,则DF=$\frac{3\sqrt{3}}{2}$.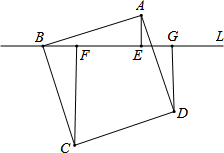 如图,过正方形ABCD的顶点B作直线L,过A,C,D作L的垂线.垂足分别为点E,F,G.若AE=2,CF=6,则CF+AE+DG的值为12.
如图,过正方形ABCD的顶点B作直线L,过A,C,D作L的垂线.垂足分别为点E,F,G.若AE=2,CF=6,则CF+AE+DG的值为12.
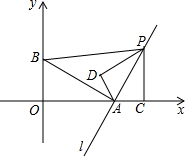 如图,在直角坐标系中,点A(4,0),点B(0,2),过点A的直线l⊥线段AB,P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处,且以点A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标是P(5,2),P(8,8),P(0,-8),P(3,-2).
如图,在直角坐标系中,点A(4,0),点B(0,2),过点A的直线l⊥线段AB,P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处,且以点A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标是P(5,2),P(8,8),P(0,-8),P(3,-2).