题目内容
17.现有两个圆,⊙O1的半径等于篮球的半径,⊙O2的半径等于一个乒乓球的半径,现将两个圆的周长都增加1米,则面积增加较多的圆是( )| A. | ⊙O1 | B. | ⊙O2 | ||
| C. | 两圆增加的面积是相同的 | D. | 无法确定 |
分析 先由L=2πR计算出两个圆半径的伸长量,然后再计算两个圆增加的面积,然后进行比较大小即可.
解答 解:设⊙O1的半径等于R,变大后的半径等于R′;⊙O2的半径等于r,变大后的半径等于r′,其中R>r.
由题意得,2πR+1=2πR′,2πr+1=2πr′,
解得R′=R+$\frac{1}{2π}$,r′=r+$\frac{1}{2π}$;
所以R′-R=$\frac{1}{2π}$,r′-r=$\frac{1}{2π}$,
所以,两圆的半径伸长是相同的,且两圆的半径都伸长$\frac{1}{2π}$.
∴⊙O1的面积=πR2,变大后的面积=$π(R+\frac{1}{2π})^{2}$,面积增加了$π(R+\frac{1}{2π})^{2}$-πR2=R+$\frac{1}{4{π}^{2}}$,
⊙O2的面积=πr2,变大后的面积=$π(r+\frac{1}{2π})^{2}$,面积增加了$π(r+\frac{1}{2π})^{2}-π{r}^{2}$=r+$\frac{1}{4{π}^{2}}$,
∵R>r,
∴R+$\frac{1}{4{π}^{2}}$>r+$\frac{1}{4{π}^{2}}$,
∴⊙O1的面积增加的多.
故选A.
点评 本题考查圆的周长的计算公式及面积计算公式.分别求出两圆半径的伸长量进行比较是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
8.下列计算不正确的是( )
| A. | (-2)-2=-$\frac{1}{4}$ | B. | ($\frac{1}{3}$)-2=9 | ||
| C. | 20050=20080 | D. | 3.2×10-4=0.00032. |
9.化简$\frac{{m}^{2}+mn}{{m}^{2}-{n}^{2}}$的结果是( )
| A. | $\frac{2m}{m-n}$ | B. | $\frac{m}{m-n}$ | C. | $\frac{m}{m+n}$ | D. | $\frac{m+n}{m-n}$ |
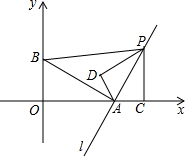 如图,在直角坐标系中,点A(4,0),点B(0,2),过点A的直线l⊥线段AB,P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处,且以点A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标是P(5,2),P(8,8),P(0,-8),P(3,-2).
如图,在直角坐标系中,点A(4,0),点B(0,2),过点A的直线l⊥线段AB,P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处,且以点A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标是P(5,2),P(8,8),P(0,-8),P(3,-2).