题目内容
5.一元二次方程x2-x-1=0和2x2-6x+5=0,这两个方程的所有实数根之和为( )| A. | 4 | B. | -4 | C. | -6 | D. | 1 |
分析 先根据根的判别式分析两个方程解的情况,可得出方程x2-x-1=0有两个不相等的实数根、方程2x2-6x+5=0没有实数根,再根据根与系数的关系即可得出方程x2-x-1=0的两个实数根之和,此题得解.
解答 解:∵在方程x2-x-1=0中,△=(-1)2-4×1×(-1)=5>0,
∴方程x2-x-1=0有两个不相等的实数根,
设方程x2-x-1=0的两个根分别为m、n,
∴m+n=1.
∵在方程2x2-6x+5=0中,△=(-6)2-4×2×5=-4<0,
∴方程2x2-6x+5=0没有实数根.
∴一元二次方程x2-x-1=0和2x2-6x+5=0的所有实数根之和为1.
故选D.
点评 本题考查了根与系数的关系以及根的判别式,利用根的判别式△=b2-4ac分析出两方程解的情况是解题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
16. 如图,在正方形ABCD外取一点E,连接AE,DE,BE,过点A作AE的垂线交ED于点P,连接BP,AE=AP=1,PB=$\sqrt{5}$,有下列结论:
如图,在正方形ABCD外取一点E,连接AE,DE,BE,过点A作AE的垂线交ED于点P,连接BP,AE=AP=1,PB=$\sqrt{5}$,有下列结论:
①△APD≌△AEB
②点B到直线AE的距离为$\sqrt{2}$;
③EB⊥ED;
④S△APD+S△APB=1+$\sqrt{6}$;
⑤S正方形ABCD=4+$\sqrt{6}$,
则正确的结论是( )
 如图,在正方形ABCD外取一点E,连接AE,DE,BE,过点A作AE的垂线交ED于点P,连接BP,AE=AP=1,PB=$\sqrt{5}$,有下列结论:
如图,在正方形ABCD外取一点E,连接AE,DE,BE,过点A作AE的垂线交ED于点P,连接BP,AE=AP=1,PB=$\sqrt{5}$,有下列结论:①△APD≌△AEB
②点B到直线AE的距离为$\sqrt{2}$;
③EB⊥ED;
④S△APD+S△APB=1+$\sqrt{6}$;
⑤S正方形ABCD=4+$\sqrt{6}$,
则正确的结论是( )
| A. | ①③④ | B. | ①②⑤ | C. | ③④⑤ | D. | ①③⑤ |
13.已知反比例函数y=$\frac{12}{x}$,当2<x<6时,y的最大整数值是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
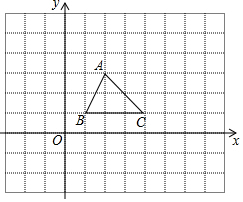 如图,在边长为1个单位长度的小正方形网格中,
如图,在边长为1个单位长度的小正方形网格中, 如图,点B、E、C、F在同一条直线上,AB=DE,AB∥DE,BE=CF.求证:AC∥DF.
如图,点B、E、C、F在同一条直线上,AB=DE,AB∥DE,BE=CF.求证:AC∥DF.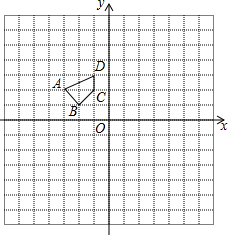 如图,在平面直角坐标系中,四边形ABCD的四个顶点分别在格点上.
如图,在平面直角坐标系中,四边形ABCD的四个顶点分别在格点上.