题目内容
5.观察下列各数:-$\frac{1}{2}$,$\frac{2}{3}$,-$\frac{3}{4}$,$\frac{4}{5}$,-$\frac{5}{6}$,…,根据它们的排列规律写出第2015个数为-$\frac{2015}{2016}$.分析 分子是从1开始连续的自然数,分母比分子多1,奇数位置为负,偶数位置为正,由此得出第n个数为(-1)n$\frac{n}{n+1}$,进一步代入求得答案即可.
解答 解:∵第n个数为(-1)n$\frac{n}{n+1}$,
∴第2015个数为-$\frac{2015}{2016}$.
故答案为:-$\frac{2015}{2016}$.
点评 此题考查数字的变化规律,发现数字之间的联系,找出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
15.一个四边形截去一个内角后变为( )
| A. | 三角形 | B. | 四边形 | C. | 五边形 | D. | 以上均有可能 |
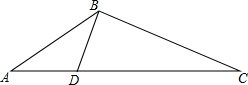 在△ABC中,D是边BC上一点,且∠ABD=∠C.
在△ABC中,D是边BC上一点,且∠ABD=∠C.