题目内容
13.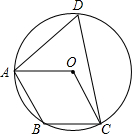 如图,点A、B、C、D都在⊙O上,且四边形OABC是平行四边形,则∠D的度数为( )
如图,点A、B、C、D都在⊙O上,且四边形OABC是平行四边形,则∠D的度数为( )| A. | 45° | B. | 60° | C. | 75° | D. | 不能确定 |
分析 根据圆周角定理得到∠D=$\frac{1}{2}$∠AOC,根据平行四边形的性质,得到∠B=∠AOC,根据圆内接四边形的性质,得到∠B+∠D=180°,得到答案.
解答 解:∠D=$\frac{1}{2}$∠AOC,
∵四边形OABC是平行四边形,
∴∠B=∠AOC,
∵四边形ABCD是圆内接四边形,
∴∠B+∠D=180°,
3∠D=180°,
∴∠D=60°,
故选:B.
点评 本题考查的是圆周角定理的应用,掌握圆周角定理、圆内接四边形的性质和平行四边形的性质是解题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
1.已知直角三角形的周长为$4+\sqrt{26}$,斜边为4,则该三角形的面积是( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{5}{4}$ |
18. 已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )
已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )
 已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )
已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
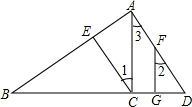 如图,已知:AB⊥AD,AC⊥BD,FG⊥BD,∠1=∠2,求证:CE⊥AB.
如图,已知:AB⊥AD,AC⊥BD,FG⊥BD,∠1=∠2,求证:CE⊥AB.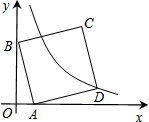 如图,在平面直角坐标系中,A(1,0),B(0,3),以AB为边在第一象限作正方形ABCD,点D在双曲线y=$\frac{k}{x}$(k≠0)上,将正方形沿x轴负方向平移m个单位长度后,点C恰好落在双曲线上,则m的值是2.
如图,在平面直角坐标系中,A(1,0),B(0,3),以AB为边在第一象限作正方形ABCD,点D在双曲线y=$\frac{k}{x}$(k≠0)上,将正方形沿x轴负方向平移m个单位长度后,点C恰好落在双曲线上,则m的值是2.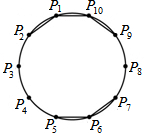 如图是P1、P2、…、P10十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接P1P2、P1P10、P9P10、P5P6、P6P7,判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?( )
如图是P1、P2、…、P10十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接P1P2、P1P10、P9P10、P5P6、P6P7,判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?( )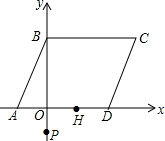 如图,?ABCD中,A(-2,0)、B(0,4),AD在x轴上,且OD=2OA.
如图,?ABCD中,A(-2,0)、B(0,4),AD在x轴上,且OD=2OA.