题目内容
15.已知:x=$\frac{1}{2+\sqrt{3}}$,y=$\frac{1}{2-\sqrt{3}}$.(1)求2x2+2y2-xy的值.
(2)若x的整数部分是a,y的小数部分是b,求5a2+(x-b)2-y的值.
分析 (1)先分母有理化求出x、y的值,求出x+y和xy的值,变形后代入求出即可;
(2)求出a、b的值,代入求出即可.
解答 解:(1)∵x=$\frac{1}{2+\sqrt{3}}$=$\frac{1×(2-\sqrt{3})}{(2+\sqrt{3})×(2-\sqrt{3})}$=2-$\sqrt{3}$,
同理y=2+$\sqrt{3}$,
∴x+y=4,xy=1,
∴2x2+2y2-xy=2[(x+y)2-2xy]-xy
=2(x+y)2-5xy
=2×42-5×1
=27;
(2)∵1<$\sqrt{3}$<2,
∴0<2-$\sqrt{3}$<1,3<2+$\sqrt{3}$<4,
∵x的整数部分为a,y的小数部分为b,
∴a=0,b=2+$\sqrt{3}$-3=$\sqrt{3}$-1,
∴5a2+(x-b)2-y=5×02+[(2-$\sqrt{3}$)-($\sqrt{3}$-1)]2-(2+$\sqrt{3}$)=19-13$\sqrt{3}$.
点评 本题考查了估算无理数的大小,二次根式的混合运算的应用,能灵活运用知识点进行计算和化简是解此题的关键.

练习册系列答案
相关题目
 如图.在Rt△ABC中,∠ACB=90°,AB=5,BC=3,AC=4,P是∠BAC,∠APC的角平分线的交点,试求P到AB边的距离.
如图.在Rt△ABC中,∠ACB=90°,AB=5,BC=3,AC=4,P是∠BAC,∠APC的角平分线的交点,试求P到AB边的距离.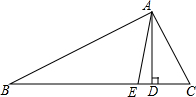 如图,三角形ABC中,∠C>∠B,AD是BC边上的高,AE是三角形中∠A的平分线.
如图,三角形ABC中,∠C>∠B,AD是BC边上的高,AE是三角形中∠A的平分线.