题目内容
4.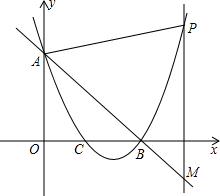 如图,已知抛物线y=x2+bx+c与直线y=-x+3交于A、B两点,点A 在y轴上,点B在x轴上,抛物线与x轴的另一交点为C,点P在点B右边的抛物线上,PM⊥x轴交直线AB于M.
如图,已知抛物线y=x2+bx+c与直线y=-x+3交于A、B两点,点A 在y轴上,点B在x轴上,抛物线与x轴的另一交点为C,点P在点B右边的抛物线上,PM⊥x轴交直线AB于M.(1)求抛物线解析式.
(2)当PM=2BC时,求M的坐标.
(3)点P运动过程中,△APM能否为等腰三角形?若能,求点P的坐标,若不能说明理由.
分析 (1)将点B(3,0)坐标代入y=x2+bx+3即可得到二次函数的解析式;
(2)根据抛物线的解析式求出BC的长,设直线PM的解析式为x=a,表示出P,M两点的坐标,再根据PM=2BC,列方程解答;
(3)△APM为等腰三角形则分别讨论PA=PM,PM=AM,PA=AM三种情况,得出符合条件的解即为点P的坐标.
解答 解:(1)当x=0时,y=3,当y=0时,x=3,
∴A,B两点的坐标为(0,3)、(3,0)
将A,B两点的坐标代入抛物线的解析式可得:
$\left\{\begin{array}{l}{c=3}\\{9a+3b+c=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{c=3}\\{b=-4}\end{array}\right.$,
∴抛物线的解析式为:y=x2-4x+3.
(2)令y=0,则x2-4x+3=0,
解得:x1=1,x2=3,∴BC=2.
设直线PM的解析式为x=a,
则P,M两点的坐标为(a,a2-4a+3),(a,-a+3)
∴PM=a2-4a+3-(-a+3)=4
解得:a1=-1(舍去),a=4,
∴M的坐标为(4,-1)
(3)若△APM为等腰三角形,进行分类讨论;
①当PA=PM时,P(m,m2-4m+3)则M(m,-m+3),
|PM|=|m2-3m|,|PA|=$\sqrt{{m}^{2}+({m}^{2}-4m)^{2}}$;
|AM|=$\sqrt{{m}^{2}+(3+m-3)^{2}}$=m$\sqrt{2}$;
由PA=PM可得|m2-3m|=$\sqrt{{m}^{2}+({m}^{2}-4m)^{2}}$,
解得m=4,m2-4m+3=3,
则P点坐标为P(4,3),
②当PA=AM时,$\sqrt{{m}^{2}+({m}^{2}-4m)^{2}}$=m$\sqrt{2}$,
解得m=3,或m=5,
当m=3时,m2-4m+3=0,由题意可知m>3,故m=3不合题意;
当m=5时,m2-4m+3=8,
故点P坐标为(5,8),
③当PA=AM时,|m2-3m|=m$\sqrt{2}$
解得m=3+$\sqrt{2}$或m=3-$\sqrt{2}$,
由题意可知m>3,故m=3-$\sqrt{2}$舍去,
当m=3+$\sqrt{2}$时,m2-4m+3=2$\sqrt{2}$+2,
故点P坐标为(3+$\sqrt{2}$,2+$\sqrt{2}$).
点评 本题是二次函数的综合题,其中涉及到的知识点有抛物线的公式的求法和等腰三角形的性质等知识点,是各地中考的热点和难点,解题时注意数形结合和分类讨论等数学思想的运用.

| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
(2)在2014年3月份日历表,圈出的四个数和为96,则这四个数中最大的为28.
| A. | 如果两个角相等,那么这两个角一定是对顶角 | |
| B. | 两个互补的角一定是邻补角 | |
| C. | 如果a2=b2,那么a=b | |
| D. | 如果两个角是对顶角,那么这两个角一定相等 |
 如图,已知△ABC的角平分线BM、CN相交于点P,那么AP能否平分∠BAC?请说明理由.由此题你能得到一个什么结论?
如图,已知△ABC的角平分线BM、CN相交于点P,那么AP能否平分∠BAC?请说明理由.由此题你能得到一个什么结论?