题目内容
14.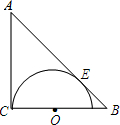 如图,在△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$+2,在BC上取一点O,以O为圆心,OC为半径作半圆与AB相切于点E.求⊙O的半径.
如图,在△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$+2,在BC上取一点O,以O为圆心,OC为半径作半圆与AB相切于点E.求⊙O的半径.
分析 连结OE,如图,设⊙O的半径为r,由于∠C=90°,AC=BC=2$\sqrt{2}$+2,则可判断△ABC为等腰直角三角形,得到AB=$\sqrt{2}$AC=4+2$\sqrt{2}$,∠B=45°,再利用切线的性质得OE⊥AB,于是可判断△OBE为等腰直角三角形,则OB=$\sqrt{2}$OE,即2$\sqrt{2}$+2-r=$\sqrt{2}$r,然后解方程即可.
解答 解:连结OE,如图,设⊙O的半径为r,
∵∠C=90°,AC=BC=2$\sqrt{2}$+2,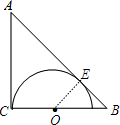
∴△ABC为等腰直角三角形,
∴AB=$\sqrt{2}$AC=$\sqrt{2}$(2$\sqrt{2}$+2)=4+2$\sqrt{2}$,∠B=45°,
∵OC为半径作半圆与AB相切于点E,
∴OE⊥AB,OC=OE=r,
∴△OBE为等腰直角三角形,
∴OB=$\sqrt{2}$OE,
即2$\sqrt{2}$+2-r=$\sqrt{2}$r,解得r=2,
即⊙C的半径为2.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了等腰直角三角形的性质.

练习册系列答案
相关题目
5.下列说法正确的是( )
| A. | 经过一点可以作两条直线 | B. | 棱柱侧面的形状可能是一个三角形 | ||
| C. | 长方体的截面形状一定是长方形 | D. | 棱柱的每条棱长都相等 |
9.在Rt△ABC和Rt△A′B′C′,∠C=∠C′=90°,AC=A′C′,AB=A′B′,下列结论错误的是( )
| A. | ∠A=∠A′ | B. | BC=B′C′ | C. | AC=B′C′ | D. | ∠B=∠B′ |
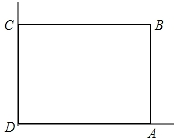 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm. 如图,在边长为2的正方形ABCD中,P为BC边上的任意一点(点P与B,C不重合),且DQ⊥AP,垂足为Q.设AP=x.DQ=y.
如图,在边长为2的正方形ABCD中,P为BC边上的任意一点(点P与B,C不重合),且DQ⊥AP,垂足为Q.设AP=x.DQ=y. 如图,△ABC中,D是BC的中点,动点E在AB边上,DF⊥DE交AC于F,连接EF,猜想:BE+CF与EF的大小关系为BE+CF>EF,并请加以证明.
如图,△ABC中,D是BC的中点,动点E在AB边上,DF⊥DE交AC于F,连接EF,猜想:BE+CF与EF的大小关系为BE+CF>EF,并请加以证明.