题目内容
 如图,已知AB、CD、EF相交于点O,AB⊥CD,∠FOD=28°,OG平分∠AOE,求∠COE、∠AOE、∠AOG的度数.
如图,已知AB、CD、EF相交于点O,AB⊥CD,∠FOD=28°,OG平分∠AOE,求∠COE、∠AOE、∠AOG的度数.考点:垂线,对顶角、邻补角
专题:
分析:先根据对顶角的性质求出∠COE的度数,再由垂线及邻补角定义得出∠AOE的度数,最后根据角平分线的定义求出∠AOG的度数.
解答:解:∵∠FOD与∠COE是对顶角,
∴∠COE=∠FOD=28°,
∴∠BOE=90°-∠COE=62°,
∴∠AOE=180°-62°=118°,
∵OG平分∠AOE,
∴∠AOG=
∠AOE=
×118°=59°.
∴∠COE=∠FOD=28°,
∴∠BOE=90°-∠COE=62°,
∴∠AOE=180°-62°=118°,
∵OG平分∠AOE,
∴∠AOG=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是垂线、邻补角及角平分线的定义,熟知角平分线的定义是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:如图,△ABC和△CDE都是等边三角形,点D在BC边上.
已知:如图,△ABC和△CDE都是等边三角形,点D在BC边上.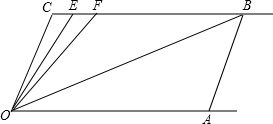 如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF
如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF 已知:如图,AD∥BE,∠1=∠2,则∠A和∠E有怎样的大小关系?为什么?
已知:如图,AD∥BE,∠1=∠2,则∠A和∠E有怎样的大小关系?为什么? 如图,点A、F、C、D在同一直线上,AB∥DE,AC=DF,AB=DE.
如图,点A、F、C、D在同一直线上,AB∥DE,AC=DF,AB=DE. 在四边形ABDC中,若∠A=∠C=90°,2∠A=3∠D,则∠B=
在四边形ABDC中,若∠A=∠C=90°,2∠A=3∠D,则∠B=