题目内容
13.三角形的一边长为3xcm,这条边上的高为xcm,其面积为ycm2,则y与x的函数关系是( )| A. | y=x2 | B. | y=2x2 | C. | y=$\frac{1}{2}$x2 | D. | y=$\frac{3}{2}$x2 |
分析 根据三角形的面积公式:面积=$\frac{1}{2}$×底×高.因此y=$\frac{1}{2}$×3x×x=$\frac{3}{2}$x2,因此可以得到函数解析式.
解答 解:由三角形的面积公式=$\frac{1}{2}$×底×高得:
y=$\frac{3}{2}$x2.
故选D.
点评 本题中掌握好三角形的面积公式是解题的关键所在,要注意的是不要丢掉三角形面积公式中的$\frac{1}{2}$.

练习册系列答案
相关题目
4.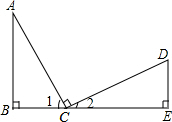 已知:如图所示,BC=ED,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
已知:如图所示,BC=ED,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
 已知:如图所示,BC=ED,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
已知:如图所示,BC=ED,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )| A. | ∠A与∠D互为余角 | B. | ∠A=∠2 | C. | △ABC≌△CED | D. | AB=CD |
1.一元二次方程y2=-6y的解是( )
| A. | -6 | B. | 0 | C. | 6 | D. | 0或-6 |
8.若分式$\frac{{x}^{2}-1}{x-1}$的值为0,则x取值为( )
| A. | x=1 | B. | x=-1 | C. | x=0 | D. | x=±1 |
18.若将分式$\frac{3{x}^{2}}{{x}^{2}-{y}^{2}}$与分式$\frac{x}{2(x-y)}$通分后,分式$\frac{x}{2(x-y)}$的分母变为2(x-y)(x+y),则分式$\frac{3x^2}{{x}^{2}-{y}^{2}}$的分子应变为( )
| A. | 6x2(x-y)2 | B. | 2(x-y) | C. | 6x2 | D. | 6x2(x+y) |
5.下列分解因式正确的是( )
| A. | x2+y2=(x+y)(x-y) | B. | (a+3)(a-3)=a2-9 | C. | a2-9=(a+3)(a-3) | D. | x3-x=x(x2-1) |
2.化简|$\sqrt{2}$-2|+$\sqrt{2}$-1的结果为( )
| A. | 2$\sqrt{2}$+1 | B. | 1 | C. | 2$\sqrt{2}$-1 | D. | -1 |
3.下列关于一元二次方程的四种解法叙述不正确的是( )
| A. | 公式法 | B. | 配方法 | C. | 加减法 | D. | 因式分解法 |
 如图所示,在△ABC中,∠A:∠B:∠BCA=1:2:3,CD⊥AB于D,AB=12,则DB等于( )
如图所示,在△ABC中,∠A:∠B:∠BCA=1:2:3,CD⊥AB于D,AB=12,则DB等于( )