题目内容
16. 如图,已知△ABC中,∠A=58°,如果:(1)O为外心;(2)O为内心;(3)O为垂心.分别求以上三种条件下的∠BOC的度数.
如图,已知△ABC中,∠A=58°,如果:(1)O为外心;(2)O为内心;(3)O为垂心.分别求以上三种条件下的∠BOC的度数.
分析 (1)根据圆周角定理直接利用∠A的度数求得∠BOC的度数即可;
(2)根据O为△ABC的内心得到∠ABO=∠OBC=$\frac{1}{2}$ABC,∠ACO=∠OCB=$\frac{1}{2}$∠ACB,根据∠ABC+∠ACB=180°-∠A=122°得到$\frac{1}{2}$(∠ABC+∠ACB)=61°,从而求得∠OBC+∠OCB=61°,进一步求得∠BOC=180°-(∠OBC+∠OCB)=119°;
(3)延长AO、BO、CO分别交三边于点D、E、F,根据垂心的定义得到AD⊥BC,BE⊥AC,CF⊥AB,从而得到∠BOD=∠ACB,∠COD=∠ABC,求得∠BOC=∠ACB+∠ABC=180°-∠A=122°.
解答 解:(1)∵点O为△ABC的外心,
∴由圆周角定理得:∠BOC=2∠A=2×58°=116°;
(2)∵O为△ABC的内心,
∴∠ABO=∠OBC=$\frac{1}{2}$ABC,∠ACO=∠OCB=$\frac{1}{2}$∠ACB,
∵∠ABC+∠ACB=180°-∠A=122°,
∴$\frac{1}{2}$(∠ABC+∠ACB)=61°,
即∠OBC+∠OCB=61°,
∴∠BOC=180°-(∠OBC+∠OCB)=119°;
(3)如图所示,延长AO、BO、CO分别交三边于点D、E、F,
则AD⊥BC,BE⊥AC,CF⊥AB,
∴∠BOD=∠ACB,∠COD=∠ABC,
∴∠BOC=∠ACB+∠ABC=180°-∠A=122°.
点评 本题考查了三角形的五心的知识及三角形的内切圆与内心,三角形得出外接圆与外心,三角形内角和定理,圆周角定理的应用,主要考查学生运用定理进行推理和计算的能力.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
7.下列式子:$\sqrt{{{(-3)}^2}},\sqrt{-5},\sqrt{8},\sqrt{{a^2}-1},\sqrt{{a^2}+1},\sqrt{4-4a+{a^2}},\root{3}{5}$中,一定是二次根式有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.$\frac{2m}{m+n}$-$\frac{m-n}{n+m}$的运算结果是( )
| A. | $\frac{3m-n}{n+m}$ | B. | -$\frac{3m-n}{n+m}$ | C. | $\frac{m-n}{m+n}$ | D. | 1 |
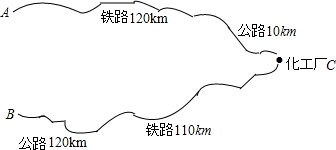 如图,某化工厂C与A、B两地有公路、跌路相连.这家工厂从A地购买一批每吨1000元的原料回工厂,制成若干每吨8000元的产品运回B地.已知公路运价为1.5元/(吨.千米),铁路运价为1.2元/(吨.千米),若这两次运输共支出铁路运费97200元,且这批产品的销售款比原料费与运输费的和多1887800元.这两次运输共支出公路运输费多少元?
如图,某化工厂C与A、B两地有公路、跌路相连.这家工厂从A地购买一批每吨1000元的原料回工厂,制成若干每吨8000元的产品运回B地.已知公路运价为1.5元/(吨.千米),铁路运价为1.2元/(吨.千米),若这两次运输共支出铁路运费97200元,且这批产品的销售款比原料费与运输费的和多1887800元.这两次运输共支出公路运输费多少元?