题目内容
19．
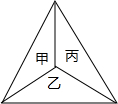如图，一只蚊子在甲、乙、丙三个房间之间飞来飞去，蚊子从一个房间随机飞到另一个房间，共飞三次．（1）若开始时蚊子在甲房间，求经过三次飞行后，蚊子回到甲房间的概率是多少？
（2）若想使蚊子经过三次飞行后回到乙房间的概率最大，则蚊子最开始时在哪个房间？请说明理由．
分析 （1）先画出树状图展示8种等可能的结果数，再找出蚊子回到甲房间的结果数，然后根据概率公式计算；
（2）由可得开始时蚊子在甲房间，经过三次飞行后，蚊子回到甲房间的概率最小，所以想使蚊子经过三次飞行后回到乙房间的概率最大，则蚊子最开始时不能在乙房间．
解答 解：（1）画树状图为：
共有8种等可能的结果数，蚊子回到甲房间的结果数为2，
所以蚊子回到甲房间的概率=$\frac{2}{8}$=$\frac{1}{4}$；
（2）由（1）得开始时蚊子在甲房间，经过三次飞行后，蚊子回到乙或丙房间的概率都是$\frac{3}{8}$，
所有想使蚊子经过三次飞行后回到乙房间的概率最大，则蚊子最开始时在甲或丙房间．
点评 本题考查了列表法或树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
7．下列式子：$\sqrt{{{（-3）}^2}}，\sqrt{-5}，\sqrt{8}，\sqrt{{a^2}-1}，\sqrt{{a^2}+1}，\sqrt{4-4a+{a^2}}，\root{3}{5}$中，一定是二次根式有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
8．$\frac{2m}{m+n}$-$\frac{m-n}{n+m}$的运算结果是（ ）
| A． | $\frac{3m-n}{n+m}$ | B． | -$\frac{3m-n}{n+m}$ | C． | $\frac{m-n}{m+n}$ | D． | 1 |