题目内容
18.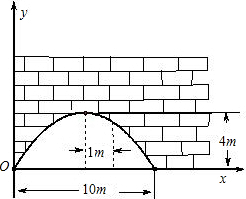 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为 4m,跨度为 10m,如图所示,把它的图形放在直角坐标系中.
有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为 4m,跨度为 10m,如图所示,把它的图形放在直角坐标系中.(1)求这条抛物线所对应的函数关系式.
(2)如图,在对称轴右边 1m 处,桥洞离水面的高是多少?
分析 (1)根据题意可以设抛物线的顶点式,然后根据函数图象过点(0,0),即可求出这条抛物线所对应的函数关系式;
(2)将x=6代入(1)中的函数解析式即可求得在对称轴右边 1m 处,桥洞离水面的高度.
解答 解:(1)设这条抛物线所对应的函数关系式是y=a(x-5)2+4,
∵该函数过点(0,0),
∴0=a(0-5)2+4,
解得,a=$-\frac{4}{25}$,
即这条抛物线所对应的函数关系式是y=-$\frac{4}{25}$(x-5)2+4;
(2)当x=6时,
y=-$\frac{4}{25}$(6-5)2+4=$\frac{96}{25}$,
即在对称轴右边 1m 处,桥洞离水面的高是$\frac{96}{25}$m.
点评 本题考查二次函数的应用,解答此类问题的关键是明确题意,求出相应的函数解析式,根据x的值,可以求得相应的函数值.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
13.在圆心角为120°的扇形AOB中,半径OA=6,则扇形AOB的面积是( )
| A. | 6π | B. | 8π | C. | 12π | D. | 24π |
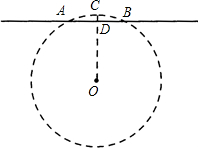 今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何.(选自《九章算术》卷第九“句股”中的第九题,1尺=10寸).
今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何.(选自《九章算术》卷第九“句股”中的第九题,1尺=10寸).