题目内容
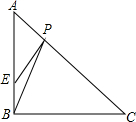 如图,在等腰直角三角形ABC中,∠ABC=90°,E是AB上一点,BE=2,AE=3BE,P是AC上一动点.则PB+PE的最小值是
如图,在等腰直角三角形ABC中,∠ABC=90°,E是AB上一点,BE=2,AE=3BE,P是AC上一动点.则PB+PE的最小值是考点:轴对称-最短路线问题
专题:
分析:由B、D关于AC对称,根据两点之间线段最短可知,连接DE,交AC于P,连接BP,则此时PB+PE的值最小,进而利用勾股定理求出即可.
解答: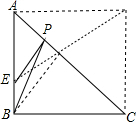 解:如图:作等腰直角三角形ABC关于AC的对称直角三角形ADC,
解:如图:作等腰直角三角形ABC关于AC的对称直角三角形ADC,
连接DE,与AC交于点P,根据两点之间,线段最短得到ED就是PB+PE的最小值,
∵等腰直角三角形ABC中,∠BAC=45°,
∴∠DAC=45°,
∴∠DAE=90°,
∵B、D关于AC对称,
∴PB=PD,
∴PB+PE=PD+PE=DE.
∵BE=2,AE=3BE,
∴AE=6,AD=AB=8,
∴DE=
=
=10.
∴PB+PE的最小值为10.
故答案为:10.
 解:如图:作等腰直角三角形ABC关于AC的对称直角三角形ADC,
解:如图:作等腰直角三角形ABC关于AC的对称直角三角形ADC,连接DE,与AC交于点P,根据两点之间,线段最短得到ED就是PB+PE的最小值,
∵等腰直角三角形ABC中,∠BAC=45°,
∴∠DAC=45°,
∴∠DAE=90°,
∵B、D关于AC对称,
∴PB=PD,
∴PB+PE=PD+PE=DE.
∵BE=2,AE=3BE,
∴AE=6,AD=AB=8,
∴DE=
| AD2+AE2 |
| 62+82 |
∴PB+PE的最小值为10.
故答案为:10.
点评:本题考查了直角三角形的性质,勾股定理,轴对称-最短路线问题等知识点的理解和掌握,能求出PE+PB=DE的长是解此题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
三角形的外心是( )
| A、各内角的平分线的交点 |
| B、各边中线的交点 |
| C、各边垂线的交点 |
| D、各边垂直平分线的交点 |
 如图,在平面直角坐标系中,直线l是第一、三象限夹角的平分线
如图,在平面直角坐标系中,直线l是第一、三象限夹角的平分线 如图,△ABC内接于⊙O,BC=m,锐角∠A=α,用m和α表示⊙O的半径R为
如图,△ABC内接于⊙O,BC=m,锐角∠A=α,用m和α表示⊙O的半径R为