题目内容
 如图,△ABC内接于⊙O,BC=m,锐角∠A=α,用m和α表示⊙O的半径R为
如图,△ABC内接于⊙O,BC=m,锐角∠A=α,用m和α表示⊙O的半径R为考点:圆周角定理,解直角三角形
专题:计算题
分析:作直径BD,连接CD,如图1,根据圆周角定理由BD为直径得∠BCD=90°,∠D=∠A=α,则根据正弦的定义得到sinD=
,则BD=
,即⊙O的半径R=
;当点A到BC的距离最大时,△ABC的面积的最大值,此时点A优弧BC的中点,如图2,AO的延长线交BC于E,连接OB,根据垂径定理的推理得
AE⊥BC,BE=
BC=
m,根据圆周角定理得∠BOE=∠BAC=α,然后在Rt△OBE中,根据正切的定义得tan∠BOE=
,可计算出OE=
,则AE=OA+OE=
+
,然后根据三角形面积公式求解
| BC |
| BD |
| m |
| sinα |
| m |
| 2sinα |
AE⊥BC,BE=
| 1 |
| 2 |
| 1 |
| 2 |
| BE |
| OE |
| m |
| 2tanα |
| m |
| 2sinα |
| m |
| 2tanα |
解答:解: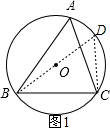 作直径BD,连接CD,如图1,
作直径BD,连接CD,如图1,
∵BD为直径,
∴∠BCD=90°,
∵∠D=∠A=α,
∴sinD=sinα=
,
∴BD=
,
∴⊙O的半径R=
;
当点A到BC的距离最大时,△ABC的面积的最大值,此时点A优弧BC的中点,如图2
AO的延长线交BC于E,连接OB,
∵点A优弧BC的中点,
∴AE⊥BC,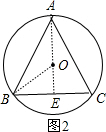
∴BE=CE=
BC=
m,
∵∠BOE=∠BAC=α,
∴在Rt△OBE中,tan∠BOE=tanα=
,
∴OE=
=
,
∴AE=OA+OE=
+
,
∴△ABC的面积=
•m•(
+
)
=(
+
)m2.
故答案为
;(
+
)m2.
 作直径BD,连接CD,如图1,
作直径BD,连接CD,如图1,∵BD为直径,
∴∠BCD=90°,
∵∠D=∠A=α,
∴sinD=sinα=
| BC |
| BD |
∴BD=
| m |
| sinα |
∴⊙O的半径R=
| m |
| 2sinα |
当点A到BC的距离最大时,△ABC的面积的最大值,此时点A优弧BC的中点,如图2
AO的延长线交BC于E,连接OB,
∵点A优弧BC的中点,
∴AE⊥BC,

∴BE=CE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BOE=∠BAC=α,
∴在Rt△OBE中,tan∠BOE=tanα=
| BE |
| OE |
∴OE=
| ||
| tanα |
| m |
| 2tanα |
∴AE=OA+OE=
| m |
| 2sinα |
| m |
| 2tanα |
∴△ABC的面积=
| 1 |
| 2 |
| m |
| 2sinα |
| m |
| 2tanα |
=(
| 1 |
| 4sinα |
| 1 |
| 4tanα |
故答案为
| m |
| 2sinα |
| 1 |
| 4sinα |
| 1 |
| 4tanα |
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了解直角三角形.

练习册系列答案
相关题目
 如图,数轴上有O,A,B,C,D五点,根据图中各点所表示的数,表示数
如图,数轴上有O,A,B,C,D五点,根据图中各点所表示的数,表示数| 18 |
| A、点O和A之间 |
| B、点A和B之间 |
| C、点B和C之间 |
| D、点C和D之间 |
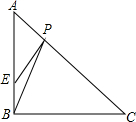 如图,在等腰直角三角形ABC中,∠ABC=90°,E是AB上一点,BE=2,AE=3BE,P是AC上一动点.则PB+PE的最小值是
如图,在等腰直角三角形ABC中,∠ABC=90°,E是AB上一点,BE=2,AE=3BE,P是AC上一动点.则PB+PE的最小值是 如图,AD∥BC,∠BAC=70°,DE⊥AC于点E,∠D=20°.
如图,AD∥BC,∠BAC=70°,DE⊥AC于点E,∠D=20°.