题目内容
 如图,在平面直角坐标系中,直线l是第一、三象限夹角的平分线
如图,在平面直角坐标系中,直线l是第一、三象限夹角的平分线(1)结合图形探索,坐标平面内任意一点P(a,b)关于第一、三象限夹角的平分线l的对称点的坐标为
(2)已知两点A(1,-3),B(-1,-4),试在直线l上确定一点C,使点C到A、B两点的距离之和最小,并求出这个最短距离.
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:(1)借助网格,根据轴对称的定义观察各点关于直线的对称点,得出规律,即可求出P(a,b)关于第一、三象限的角平分线l的对称点P'的坐标.
(2)作出B点关于直线l对称点D,连接AD,交平分线l于C,则点C到A、B两点的距离之和最小,根据勾股定理即可求得AD的长.
(2)作出B点关于直线l对称点D,连接AD,交平分线l于C,则点C到A、B两点的距离之和最小,根据勾股定理即可求得AD的长.
解答:解:(1)由图可知,(1,0)的对称点是(0,1),(2,1)的对称点是(1,2)…,
所以P(a,b)关于第一、三象限夹角的平分线l的对称点的坐标为(b,a).
(2)作出B点关于直线l对称点D,连接AD,交平分线l于C,则点C到A、B两点的距离之和最小,
∴CD=BC,
∴AC+BC=CD+AC=AD.
∵B点和D点关于直线l对称,
∴D(-4,-1),
∵A(1,-3),
∴AD=
2=

故答案为(b,a).
所以P(a,b)关于第一、三象限夹角的平分线l的对称点的坐标为(b,a).
(2)作出B点关于直线l对称点D,连接AD,交平分线l于C,则点C到A、B两点的距离之和最小,
∴CD=BC,
∴AC+BC=CD+AC=AD.
∵B点和D点关于直线l对称,
∴D(-4,-1),
∵A(1,-3),
∴AD=
| (1+4)2+(-1+3) |
| 29 |

故答案为(b,a).
点评:此题考查了规律的探索和轴对称的性质,先借助网格,根据轴对称的定义得出规律,是本题的重点.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
下列说法正确的是( )
| A、近似数2.4×104精确到十分位 |
| B、将数60340精确到千位是6.0×104 |
| C、按科学记数法表示的数6.05×105,其原数是60500 |
| D、近似数8.1750是精确到0.001 |
 已知:线段a,画出一条线段,使它等于2a.
已知:线段a,画出一条线段,使它等于2a.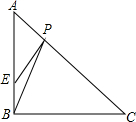 如图,在等腰直角三角形ABC中,∠ABC=90°,E是AB上一点,BE=2,AE=3BE,P是AC上一动点.则PB+PE的最小值是
如图,在等腰直角三角形ABC中,∠ABC=90°,E是AB上一点,BE=2,AE=3BE,P是AC上一动点.则PB+PE的最小值是