Question

20．如图，在平面直角坐标系xOy中，矩形OABC的OA、OC两边在坐标轴上，点B（4，2），D、E分别为BC、OA的中点，边AB、BC与双曲线y=$\frac{2}{x}$（x＞0）交于点F、G，点P在双曲线上点F、G两点之间，过点P作x轴的垂线交BC于点H，交直线CE于点I，连接DP、PA．设点P的横坐标为m．
（1）请直接写出直线CE的解析式；
（2）探索点P的位置时，小明发现：当点P在与G重合或D、P、I共线时，PD=PI．进而猜想：对于任意一点P．PD=PI也成立．请你判断该猜想是否正确，并说明理由；
（3）当m为何值时，AP+PI最小，并求出这个最小值．

Answer 1

分析 （1）先求出C、E的坐标，再利用待定系数法求出直线CE的解析式即可；
（2）设P（m，n），根据点P在双曲线y=$\frac{2}{x}$（x＞0）上得出mn=2，用mn表示出PI，DH，PH的长，再根据勾股定理得出PD的长，进而可得出结论；
（3）连接DA，根据AP+PI=AP+PD≥DA可知A、P、D共线时取等号，直线DA的方程为y=-x+4，联立方程组$\left\{\begin{array}{l}mn=2\\ n=-m+4\end{array}\right.$求出m的值即可得出结论．

解答 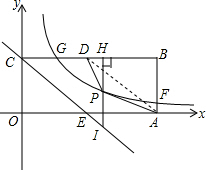解：（1）∵矩形OABC的OA、OC两边在坐标轴上，点B（4，2），E为OA的中点，
∴C（0，2），E（2，0），
∴设直线CE的解析式为y=kx+b（k≠0），
∴$\left\{\begin{array}{l}b=2\\ 2k+b=0\end{array}\right.$，解得$\left\{\begin{array}{l}b=2\\ k=-1\end{array}\right.$，
∴直线CE的解析式为y=-x+2；

（2）设P（m，n），
∵点P在双曲线y=$\frac{2}{x}$（x＞0）上，
∴mn=2，PI=n-（-m+2）=m+n-2，DH²=（2-m）²，PH²=（2-n）²，
∴PD²=DH²+PH²=（m-2）²+（2-n）²=（m+n-2）²，即PD=m+n-2．
∴PD=PI；

（3）连接DA，
∵AP+PI=AP+PD≥DA，
∴A、P、D共线时取等号．
直线DA的方程为y=-x+4，联立方程组$\left\{\begin{array}{l}mn=2\\ n=-m+4\end{array}\right.$，解得m=2+$\sqrt{2}$或m=2-$\sqrt{2}$（舍去）．
∴当m=2+$\sqrt{2}$时，AP+PI有最小值=AD=$\sqrt{{AB}^{2}+{BD}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$．

点评 本题考查的是反比例函数综合题，涉及到反比例函数图象上点的坐标特点、矩形的性质及用待定系数法求一次函数的解析式、勾股定理等知识，难度适中．