题目内容
8．我们是这样研究一个数绝对值的性质的：当a＞0时，如a=6，则|a|=|6|=6，此时a的绝对值是它本身；当a=0时，|a|=0，此时a的绝对值是零；当a＜0时，如a=-6，则|a|=|-6|=6，此时a的绝对值是它的相反数．这种分析问题的方法所体现的数学思想是（ ）| A． | 转化思想 | B． | 分类思想 | C． | 数形结合思想 | D． | 公理化思想 |
分析 根据负数的绝对值是它的相反数，正数的绝对值是它本身，0的绝对值是0，即可解答．
解答 解：∵当a＞0时，如a=6，则|a|=|6|=6，此时a的绝对值是它本身；
当a=0时，|a|=0，此时a的绝对值是零；
当a＜0时，如a=-6，则|a|=|-6|=6，此时a的绝对值是它的相反数．
∴采用了分类讨论的方法，
故选：B．
点评 本题考查了绝对值，解决本题的关键是熟记负数的绝对值是它的相反数，正数的绝对值是它本身，0的绝对值是0．
练习册系列答案
相关题目
18．下列函数中，y是x的反比例函数有（ ）
（1）y=3x；（2）y=-$\frac{2}{x}$；（3）$y=\frac{x}{3}$；（4）-xy=3；（5）$y=\frac{2}{x+1}$；（6）$y=\frac{1}{x^2}$；（7）y=2x-2；（8）$y=\frac{k}{x}$．
（1）y=3x；（2）y=-$\frac{2}{x}$；（3）$y=\frac{x}{3}$；（4）-xy=3；（5）$y=\frac{2}{x+1}$；（6）$y=\frac{1}{x^2}$；（7）y=2x-2；（8）$y=\frac{k}{x}$．
| A． | （2）（4） | B． | （2）（3）（5）（8） | C． | （2）（7）（8） | D． | （1）（3）（4）（6） |
3．
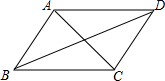如图，在平行四边形ABCD中，连接对角线AC、BD，图中的全等三角形的对数（ ）
如图，在平行四边形ABCD中，连接对角线AC、BD，图中的全等三角形的对数（ ）| A． | 1对 | B． | 2对 | C． | 3对 | D． | 4对 |
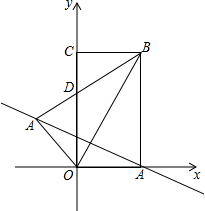如图，矩形OABC在平面直角坐标系中，若OA，OC的长满足|OA-2|+（OC-2$\sqrt{3}$）2=0．