题目内容
10.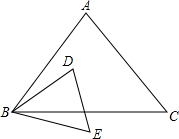 如图,在△ABC和△DBE中,$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{AC}{DE}$=$\frac{3}{2}$.
如图,在△ABC和△DBE中,$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{AC}{DE}$=$\frac{3}{2}$.(1)若△ABC和△DBE的周长之差为6.求△ABC的周长;
(2)若△ABC和△DBE的面积之和为260cm2,求△DBE的面积.
分析 (1)根据相似三角形的判定得到△ABC∽△BDE,由相似三角形的性质得到△ABC的周长:△DBE的周长=$\frac{3}{2}$,求得△ABC的周长=$\frac{3}{2}$△DBE的周长,根据已知条件得到△ABC的周长-△DBE的周长=$\frac{1}{2}$△DBE的周长=6,于是得到结论;
(2)根据相似三角形的性质得到$\frac{{S}_{△ABC}}{{S}_{△BDE}}$=($\frac{3}{2}$)2=$\frac{9}{4}$,求得S△ABC=$\frac{9}{4}$S△BDE,根据已知条件得到$\frac{5}{4}$S△BDE=260,于是得到结论.
解答 解:(1)∵在△ABC和△DBE中,$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{AC}{DE}$=$\frac{3}{2}$.
∴△ABC∽△BDE,
∴△ABC的周长:△DBE的周长=$\frac{3}{2}$,
∴△ABC的周长=$\frac{3}{2}$△DBE的周长,
∵△ABC和△DBE的周长之差为6,
∴△ABC的周长-△DBE的周长=$\frac{1}{2}$△DBE的周长=6,
∴△DBE的周长=12,
∴△ABC的周长=18;
(2)∵△ABC∽△BDE,
∴$\frac{{S}_{△ABC}}{{S}_{△BDE}}$=($\frac{3}{2}$)2=$\frac{9}{4}$,
∴S△ABC=$\frac{9}{4}$S△BDE,
∵△ABC和△DBE的面积之和为260cm2,
∴$\frac{5}{4}$S△BDE=260,
∴S△DBE=208cm2.
点评 本题考查了相似三角形的判定和性质,三角形的面积和周长的计算,熟练掌握相似三角形的性质是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 75m | B. | 50m | C. | 75$\sqrt{2}$m | D. | 50$\sqrt{2}$m |
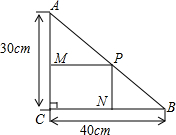 如图,在Rt△ABC的内部作一个矩形CMPN,其中CM、CN分别在两直角边上,设CM=xcm,那么CN的长为( )
如图,在Rt△ABC的内部作一个矩形CMPN,其中CM、CN分别在两直角边上,设CM=xcm,那么CN的长为( )| A. | 40-$\frac{4}{3}$x | B. | 40-$\frac{3}{2}$x | C. | 30-$\frac{4}{3}$x | D. | 30-$\frac{3}{4}$x |
| A. | 32与-32 | B. | (-2)2与-22 | C. | |-2|与-|+2| | D. | (-2)3与-23 |
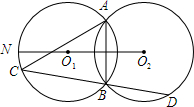 已知:两等圆⊙O1与⊙O2相交于点A、B,若点O1在⊙O2外,延长O2O1交⊙O1于点N,在劣弧$\widehat{NB}$上任取一点C(点C与点B不重合),CB的延长线交⊙O2于点D,如图所示,连结AC,试比较AC与AB的大小.
已知:两等圆⊙O1与⊙O2相交于点A、B,若点O1在⊙O2外,延长O2O1交⊙O1于点N,在劣弧$\widehat{NB}$上任取一点C(点C与点B不重合),CB的延长线交⊙O2于点D,如图所示,连结AC,试比较AC与AB的大小.