题目内容
8.解不等式组:$\left\{\begin{array}{l}{\frac{x-1}{2}≥\frac{2x-5}{3}}\\{3x>5+2(x-1)}\end{array}\right.$并把解集在数轴上表示出来.分析 先求出每个不等式的解集,再求出不等式组的解集,最后在数轴上表示出来即可.
解答 解:$\left\{\begin{array}{l}{\frac{x-1}{2}≥\frac{2x-5}{3}①}\\{3x>5+2(x-1)②}\end{array}\right.$
∵解不等式①,得:x≤7
解不等式②,得:x>3,
∴原不等式组的解集为3<x≤7,
把不等式的解集在数轴上表示为: .
.
点评 本题考查了解一元一次不等式组,在数轴上表示不等式组的解集等知识点,能求出不等式组的解集是解此题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
19.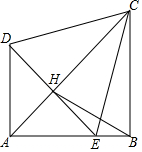 将两个等腰Rt△ADE,Rt△ABC(其中∠DAE=∠ABC=90°,AB=BC,AD=AE)如图放置在一起,点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:
将两个等腰Rt△ADE,Rt△ABC(其中∠DAE=∠ABC=90°,AB=BC,AD=AE)如图放置在一起,点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:
①AC垂直平分DE;
②CDE为等边三角形;
③tan∠BCD=$\frac{AB}{BE}$;
④$\frac{{S}_{△EBC}}{{S}_{△EHC}}$=$\frac{\sqrt{3}}{3}$
正确的结论是( )
 将两个等腰Rt△ADE,Rt△ABC(其中∠DAE=∠ABC=90°,AB=BC,AD=AE)如图放置在一起,点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:
将两个等腰Rt△ADE,Rt△ABC(其中∠DAE=∠ABC=90°,AB=BC,AD=AE)如图放置在一起,点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:①AC垂直平分DE;
②CDE为等边三角形;
③tan∠BCD=$\frac{AB}{BE}$;
④$\frac{{S}_{△EBC}}{{S}_{△EHC}}$=$\frac{\sqrt{3}}{3}$
正确的结论是( )
| A. | 只有①② | B. | 只有③④ | C. | 只有①②④ | D. | ①②③④ |
16.小明有两双不同颜色的拖鞋放在床前,拖鞋分左右脚.他半夜起床抹黑穿拖鞋,则他左右脚穿对同颜色鞋子的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
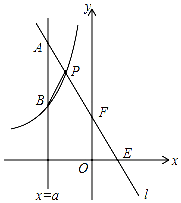 如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{4}{x}$
如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{4}{x}$ 如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=5米,AB=7米,∠MAD=45°,∠MBC=30°,求警示牌的高CD为多少米?(结果保留根号)
如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=5米,AB=7米,∠MAD=45°,∠MBC=30°,求警示牌的高CD为多少米?(结果保留根号)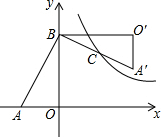 如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数y=$\frac{k}{x}$的图象恰好经过斜边A′B的中点C,S△ABO=16,tan∠BAO=2,则k的值为( )
如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数y=$\frac{k}{x}$的图象恰好经过斜边A′B的中点C,S△ABO=16,tan∠BAO=2,则k的值为( )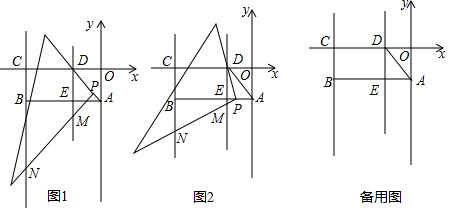
 如图,已知△ABC,求作:⊙O,使得⊙O经过A、C两点,且圆心O落在AB边上.(要求:尺规作图,保留作图痕迹,不写作法)
如图,已知△ABC,求作:⊙O,使得⊙O经过A、C两点,且圆心O落在AB边上.(要求:尺规作图,保留作图痕迹,不写作法)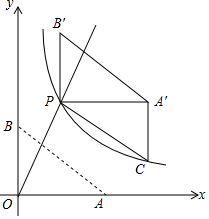 如图,直线y=k1x(x≥0)与双曲线y=$\frac{k_2}{x}$(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A'PB'.过点A'作A'C∥y轴交双曲线于点C.
如图,直线y=k1x(x≥0)与双曲线y=$\frac{k_2}{x}$(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A'PB'.过点A'作A'C∥y轴交双曲线于点C.