题目内容
13．
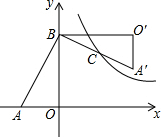如图，在Rt△AOB中，两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，将△AOB绕点B逆时针旋转90°后得到△A′O′B．若反比例函数y=$\frac{k}{x}$的图象恰好经过斜边A′B的中点C，S△ABO=16，tan∠BAO=2，则k的值为（ ）| A． | 20 | B． | 22 | C． | 24 | D． | 26 |
分析 在Rt△AOB中，由tan∠BAO=$\frac{OB}{OA}$=2，可以假设OB=2k，OA=k，由题意$\frac{1}{2}$•k•2k=16，推出k=4，可得OA=4，OB=8，C（4，6），由此即可解决问题．
解答 解：在Rt△AOB中，∵tan∠BAO=$\frac{OB}{OA}$=2，
∴可以假设OB=2k，OA=k，
∴$\frac{1}{2}$•k•2k=16，
∴k=4或-4（舍弃），
∴OA=4，OB=8，
∵BC=CA′，
∴C（4，6），
∵反比例函数y=$\frac{k}{x}$的图象经过点C，
∴k=24．
故选C．
点评 本题考查坐标与图形的变化，旋转变换、解直角三角形等知识，解题的关键是求出点C的坐标，属于中考常考题型．
练习册系列答案
相关题目
3．
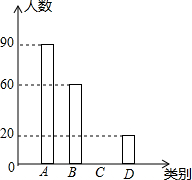雾霾天气已经成为人们普遍关注的话题，雾霾不仅仅影响人们的出行，还影响着人们的健康．在2017年2月周末休息期间，某校九年级一班综合实践小组的同学以“雾霾天气的主要成因”为主题，随机调查了太原市部分市民的观点，并对调查结果进行了整理，绘制了如下不完整的统计表及统计图，观察并回答下列问题：
（1）请你求出本次被调查市民的人数及m，n的值，并补全条形统计图；
（2）若该市有800万人口，请你估计持有B，C两类看法的市民共有多少人？
（3）小明同学在四个质地、大小、形状都完全相同的小球上标记A，B，C，D代表四个雾霾天气的主要成因中，放在一个不透明的盒子中，他先随机抽取一个小球，放回去，再随机抽取一个小球，请用画树状图或列表的方法，求出小颖同学刚好抽到B和D的概率．（用A，B，C，D表示各项目）
雾霾天气已经成为人们普遍关注的话题，雾霾不仅仅影响人们的出行，还影响着人们的健康．在2017年2月周末休息期间，某校九年级一班综合实践小组的同学以“雾霾天气的主要成因”为主题，随机调查了太原市部分市民的观点，并对调查结果进行了整理，绘制了如下不完整的统计表及统计图，观察并回答下列问题：| 类别 | 雾霾天气的主要成因 | 百分比 |
| A | 工业污染 | 45% |
| B | 汽车尾气排放 | m |
| C | 城中村燃煤问题 | 15% |
| D | 其他（绿化不足等） | n |
（2）若该市有800万人口，请你估计持有B，C两类看法的市民共有多少人？
（3）小明同学在四个质地、大小、形状都完全相同的小球上标记A，B，C，D代表四个雾霾天气的主要成因中，放在一个不透明的盒子中，他先随机抽取一个小球，放回去，再随机抽取一个小球，请用画树状图或列表的方法，求出小颖同学刚好抽到B和D的概率．（用A，B，C，D表示各项目）
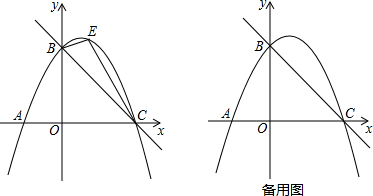
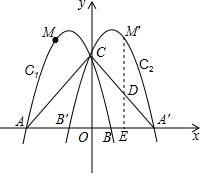如图，抛物线C1：y=ax2+bx+4与x轴交于A（-3，0），B两点，与y轴交于点C，点M（-$\frac{3}{2}$，5）是抛物线C1上一点，抛物线C2与抛物线C1关于y轴对称，点A、B、M关于y轴的对称点分别为点A′、B′、M′．
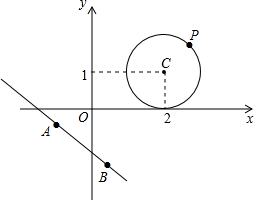阅读材料：