题目内容
商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价2元,商场平均每天可多售出 4件.设每件商品降价x元.据此规律,请回答:
(1)每件商品降价多少元时,商场日盈利可达到2100元?
(2)商场日盈利能否达到2200元?请说明理由.
(1)每件商品降价多少元时,商场日盈利可达到2100元?
(2)商场日盈利能否达到2200元?请说明理由.
考点:一元二次方程的应用
专题:销售问题
分析:(1)根据总利润=数量×每件的利润建立方程求出其解即可;
(2)设总盈利为W元,根据总利润=数量×每件的利润表示出W与x之间的关系式,就可以求出最大值.
(2)设总盈利为W元,根据总利润=数量×每件的利润表示出W与x之间的关系式,就可以求出最大值.
解答:解:(1)由题意,得
(30+4×
)(50-x)=2100,
解得:x1=20,x2=15.
∵为了减少库存,
∴每件商品降价20元;
(2)设总盈利为W元,由题意,得
W=(30+4×
)(50-x),
=-2x2+70x+1500,
=-2(x-
)2+2112.5.
∴a=-2<0,
∴W有最大值,
∴x=
时,W最大=2112.5<2200.
∴商场日盈利不能达到2200元.
(30+4×
| x |
| 2 |
解得:x1=20,x2=15.
∵为了减少库存,
∴每件商品降价20元;
(2)设总盈利为W元,由题意,得
W=(30+4×
| x |
| 2 |
=-2x2+70x+1500,
=-2(x-
| 35 |
| 2 |
∴a=-2<0,
∴W有最大值,
∴x=
| 35 |
| 2 |
∴商场日盈利不能达到2200元.
点评:本题考查了利润问题的数量关系的运用,列一元二次方程解实际问题的运用,二次函数的解析式的运用,二次函数的性质的运用,解答时由总利润=数量×每件的利润建立方程是关键.

练习册系列答案
相关题目
 如图,已知圆锥侧面展开图的扇形面积为65π cm2,扇形的弧长为10π cm,则圆锥的高是( )
如图,已知圆锥侧面展开图的扇形面积为65π cm2,扇形的弧长为10π cm,则圆锥的高是( )| A、5cm | B、10cm |
| C、12cm | D、13cm |
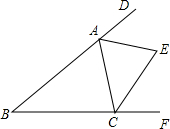 如图所示,在△ABC中,∠B=48°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC的度数为
如图所示,在△ABC中,∠B=48°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC的度数为 如图,△ABC中,∠B=90°,AB=6,BC=8,点P从点A开始沿边AB向点B以km/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动,问:
如图,△ABC中,∠B=90°,AB=6,BC=8,点P从点A开始沿边AB向点B以km/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动,问: 如图1是我国古代著名的“赵爽 弦图”的示意图,它是由四个全等的直角三角形围成.若较短的直角边BC=2.5,将四个直角三角形中较长的直角边分别向外延长一倍,得到图2所示的“数学风车”,若△BCD的周长是15,则这个风车的外围周长是
如图1是我国古代著名的“赵爽 弦图”的示意图,它是由四个全等的直角三角形围成.若较短的直角边BC=2.5,将四个直角三角形中较长的直角边分别向外延长一倍,得到图2所示的“数学风车”,若△BCD的周长是15,则这个风车的外围周长是