题目内容
有一块直角三角形纸片，两直角边AB=6，BC=8，将该纸片折叠，使直角边AB落在斜边AC上，折痕为AD，则BD= ．
考点：翻折变换（折叠问题）
专题：
分析：作出图形，利用勾股定理列式求出AC，再根据翻折变换的性质可得AE=AB，DE=BD，然后求出CE，设BD=x，表示出CD，再利用勾股定理列出方程求解即可．
解答：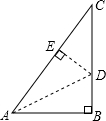
解：如图，∵两直角边AB=6，BC=8，
∴斜边AC=
=
=10，
由翻折的性质得，AE=AB，DE=BD，
∴CE=AC-AE=10-6=4，
设BD=x，则CD=8-x，
在Rt△CDE中，DE2+CE2=CD2，
即x2+42=（8-x）2，
解得x=3，
即BD=3．
故答案为：3．
解：如图，∵两直角边AB=6，BC=8，∴斜边AC=
| AB2+BC2 |
| 62+82 |
由翻折的性质得，AE=AB，DE=BD，
∴CE=AC-AE=10-6=4，
设BD=x，则CD=8-x，
在Rt△CDE中，DE2+CE2=CD2，
即x2+42=（8-x）2，
解得x=3，
即BD=3．
故答案为：3．
点评：本题考查了翻折变换的性质，勾股定理，熟记性质并利用勾股定理列出方程是解题的关键，作出图形更形象直观．
练习册系列答案
阅读快车系列答案
相关题目
△ABC中，已知BC=6，点D是BC边上的中点，AD=5，点P为线段AD上一点（与A、D不重合），过P作EF∥BC分别交AB，AC于点E、F，过E、F分别作EG∥AD，FH∥AD交BC边于点G．
如图，在边长为1个单位长度的小正方形组成的网格中，按要求作图．
如图所示，已知AB为⊙O的直径，半径OC⊥AB，E为OB上一点，弦AD⊥CE交OC于点F，猜想OE与OF的数量关系，并说明你的理由．当角度在0°到90°之间变化时，函数值随着角度的增大而增大的三角函数是（ ）
| A、正弦和余弦 |
| B、正弦和正切 |
| C、余弦和正切 |
| D、正弦、余弦和正切 |