题目内容
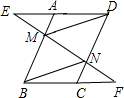 已知,如图,在平行四边形ABCD中,点M,N分别在边AB,DC上,作直线MN,分别交DA和BC的延长线于点E,F,且AE=CF.
已知,如图,在平行四边形ABCD中,点M,N分别在边AB,DC上,作直线MN,分别交DA和BC的延长线于点E,F,且AE=CF.(1)求证:△AEM≌△CFN;
(2)求证:四边形BNDM是平行四边形.
考点:平行四边形的判定与性质,全等三角形的判定与性质
专题:证明题
分析:(1)利用“平行四边形的对边相互平行”和平行线的性质易推知∠1=∠3,∠E=∠F,然后结合已知条件,由AAS证得结论;
(2)利用(1)中全等三角形的对应边相等推知AM=CN,则结合平行四边形的性质可以得到BM=DN,则“有一组对边相互平行且相等的四边形是平行四边形”证得结论.
(2)利用(1)中全等三角形的对应边相等推知AM=CN,则结合平行四边形的性质可以得到BM=DN,则“有一组对边相互平行且相等的四边形是平行四边形”证得结论.
解答: 证明:(1)如图,∵四边形ABCD是平行四边形,
证明:(1)如图,∵四边形ABCD是平行四边形,
∴AD∥BC即ED∥BF,AB∥DC,
∴∠E=∠F,∠2=∠3.
又∠1=∠2,
∴∠1=∠3.
在△AEM与△CFN中,
,
∴△AEM≌△CFN(AAS);
(2)由(1)知:△AEM≌△CFN,则AM=CN.
又∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴AB-AM=CD-CN即MB=ND,MB∥ND,
∴四边形BNDM是平行四边形.
 证明:(1)如图,∵四边形ABCD是平行四边形,
证明:(1)如图,∵四边形ABCD是平行四边形,∴AD∥BC即ED∥BF,AB∥DC,
∴∠E=∠F,∠2=∠3.
又∠1=∠2,
∴∠1=∠3.
在△AEM与△CFN中,
|
∴△AEM≌△CFN(AAS);
(2)由(1)知:△AEM≌△CFN,则AM=CN.
又∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴AB-AM=CD-CN即MB=ND,MB∥ND,
∴四边形BNDM是平行四边形.
点评:本题考查了平行四边形的判定与性质,全等三角形的判定与性质.凡是可以用平行四边形知识证明的问题,不要再回到用三角形全等证明,应直接运用平行四边形的性质和判定去解决问题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
 如图,请画出△ABC关于点A的对称图形.
如图,请画出△ABC关于点A的对称图形.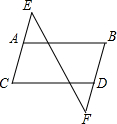 如图,现有以下3句话:①AB∥CD,②∠B=∠C.③∠E=∠F.请以其中2句话为条件,第三句话为结论构造命题.
如图,现有以下3句话:①AB∥CD,②∠B=∠C.③∠E=∠F.请以其中2句话为条件,第三句话为结论构造命题.