题目内容
用指定的方法解下列方程:
(1)x2+4x-1=0(用配方法);
(2)2x2-8x+3=0(用公式法).
(1)x2+4x-1=0(用配方法);
(2)2x2-8x+3=0(用公式法).
考点:解一元二次方程-配方法,解一元二次方程-公式法
专题:计算题
分析:(1)先把常数项移到方程左边,再两边加上4得到x2+4x+4=5,然后把方程左边写成完全平方式,再利用直接开平方法解方程;
(2)先计算判别式的值,然后代入一元二次方程的求根公式中求解.
(2)先计算判别式的值,然后代入一元二次方程的求根公式中求解.
解答:(1)解:x2+4x=1,
x2+4x+4=5
(x+2)2=5,
x+2=±
,
所以x1=-2+
,x2=-2-
;
(2)解:∵a=2,b=-8,c=3,
∴△=b2-4ac=(-8)2-4×2×3=40
∴x=
=
,
∴x1=
,x2=
.
x2+4x+4=5
(x+2)2=5,
x+2=±
| 5 |
所以x1=-2+
| 5 |
| 5 |
(2)解:∵a=2,b=-8,c=3,
∴△=b2-4ac=(-8)2-4×2×3=40
∴x=
8±
| ||
| 2×2 |
4±
| ||
| 2 |
∴x1=
4+
| ||
| 2 |
4-
| ||
| 2 |
点评:本题考查了解一元二次方程-配方法:将一元二次方程配成(x+m)2=n的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法.也考查了解一元二次方程-公式法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,∠1=∠2,∠C=∠D.求证:∠A=∠F.
如图,∠1=∠2,∠C=∠D.求证:∠A=∠F.
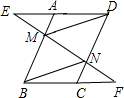 已知,如图,在平行四边形ABCD中,点M,N分别在边AB,DC上,作直线MN,分别交DA和BC的延长线于点E,F,且AE=CF.
已知,如图,在平行四边形ABCD中,点M,N分别在边AB,DC上,作直线MN,分别交DA和BC的延长线于点E,F,且AE=CF. 如图,已知正方形ABCD的边长是2,点E在DC上,△ADE经顺时针旋转后与△ABF重合.
如图,已知正方形ABCD的边长是2,点E在DC上,△ADE经顺时针旋转后与△ABF重合.