题目内容
探究规律,解决问题:
(1)化简:(m-1)(m+1)= ,(m-1)(m2+m+1)= .
(2)化简:(m-1)(m3+m2+m+1),写出化简过程.
(3)化简:(m-1)(mn+mn-1+mn-2+…+1)= .(n为正整数,mn+mn-1+mn-2+…+1为n+1项多项式)
(4)利用以上结果,计算1+3+32+33+…+3100的值.
(1)化简:(m-1)(m+1)=
(2)化简:(m-1)(m3+m2+m+1),写出化简过程.
(3)化简:(m-1)(mn+mn-1+mn-2+…+1)=
(4)利用以上结果,计算1+3+32+33+…+3100的值.
考点:多项式乘多项式
专题:规律型
分析:(1)(2)根据多项式乘多项式的运算法则进行计算即可;
(3)根据(1)(2)得出的规律可直接得出答案;
(4)根据(3)的出的规律可直接代数进行计算即可.
(3)根据(1)(2)得出的规律可直接得出答案;
(4)根据(3)的出的规律可直接代数进行计算即可.
解答:解:(1)(m-1)(m+1)=m2-1;
(m-1)(m2+m+1)=m3-1;
故答案为:m2-1;m3-1;
(2)(m-1)(m3+m2+m+1)
=m4+m3+m2+m-m3-m2-m-1
=m4-1;
(3)(m-1)(mn-1+mn-2+…m2+m+1)=mn+1-1;
故答案为:mn+1-1;
(4)根据(3)得出的规律可得:
1+3+32+33+…+3100=3101-1.
(m-1)(m2+m+1)=m3-1;
故答案为:m2-1;m3-1;
(2)(m-1)(m3+m2+m+1)
=m4+m3+m2+m-m3-m2-m-1
=m4-1;
(3)(m-1)(mn-1+mn-2+…m2+m+1)=mn+1-1;
故答案为:mn+1-1;
(4)根据(3)得出的规律可得:
1+3+32+33+…+3100=3101-1.
点评:本题主要考查多项式乘以多项式的法则,多项式乘以多项式的法则,可表示为(a+b)(m+n)=am+an+bm+bn,注意不要漏项,漏字母.

练习册系列答案
相关题目
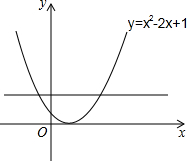 如果抛物线m的顶点在抛物线n上,同时抛物线n的顶点在抛物线m上,那么我们就称抛物线m与n为交融抛物线.
如果抛物线m的顶点在抛物线n上,同时抛物线n的顶点在抛物线m上,那么我们就称抛物线m与n为交融抛物线.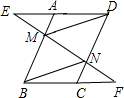 已知,如图,在平行四边形ABCD中,点M,N分别在边AB,DC上,作直线MN,分别交DA和BC的延长线于点E,F,且AE=CF.
已知,如图,在平行四边形ABCD中,点M,N分别在边AB,DC上,作直线MN,分别交DA和BC的延长线于点E,F,且AE=CF.