题目内容
 如图,矩形ABCD的边长AB=2,BC=3,点P是AD边上一动点(P异于A,D),Q是BC边上的任意一点连AQ,DQ,过P作PE∥DQ,交AQ于E,作PF∥AQ交DQ于F.
如图,矩形ABCD的边长AB=2,BC=3,点P是AD边上一动点(P异于A,D),Q是BC边上的任意一点连AQ,DQ,过P作PE∥DQ,交AQ于E,作PF∥AQ交DQ于F.①求证:△APE∽△ADQ.
②设AP的长为x,试求△PEF的面积y关于x的函数关系式.
③当Q在何处时,△ADQ的周长最小?
考点:相似三角形的判定与性质,二次函数的最值,矩形的性质
专题:
分析:(1)根据PE∥QD得出两三角形相似.
(2)根据相似三角形的面积之比等于相似比得平方及S△PEF=
S平行四边形PEQF,列出式子求出△PEF的面积y关于x的函数关系式.
(3)△ADQ中,AD长为定值,因此要使△ADQ的周长最小,AQ+QD需最小,可根据轴对称图形的性质和两点间线段最短为依据来确定Q点的位置.
(2)根据相似三角形的面积之比等于相似比得平方及S△PEF=
| 1 |
| 2 |
(3)△ADQ中,AD长为定值,因此要使△ADQ的周长最小,AQ+QD需最小,可根据轴对称图形的性质和两点间线段最短为依据来确定Q点的位置.
解答:(1)证明:∵PE∥DQ
∴△APE∽△ADQ;
(2)解:同(1)可证△APE∽△ADQ,
△PDF∽△ADQ,
S△PEF=
S平行四边形PEQF,
设AP的长为x,根据相似三角形的面积之比等于相似比得平方,
∴
=(
)2,
=(
)2,
∵S△AQD=
AD×AB=
×3×2=3,
得S△PEF=
S平行四边形PEQF
=
(S△AQD-S△AEP-S△DFP),
=
×[3-(
)2×3-(
)2×3],
=
(-
x2+2x),
=-
x2+x
∴y=-
x2+x.
(3)解:如图,作A关于直线BC的对称点A′,连DA′交BC于Q,则这个点Q就是使△ADQ周长最小的点,

∵BQ∥AD,点B为AA′中点,
∴BQ为△A′AD的中位线,
此时Q是BC的中点,
最小周长为AD+A′D=3+
=3+
=3+5=8.
∴△APE∽△ADQ;
(2)解:同(1)可证△APE∽△ADQ,
△PDF∽△ADQ,
S△PEF=
| 1 |
| 2 |
设AP的长为x,根据相似三角形的面积之比等于相似比得平方,
∴
| S△AEP |
| S△AQD |
| x |
| 3 |
| S△DPF |
| S△ADQ |
| 3-x |
| 3 |
∵S△AQD=
| 1 |
| 2 |
| 1 |
| 2 |
得S△PEF=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| x |
| 3 |
| 3-x |
| 3 |
=
| 1 |
| 2 |
| 2 |
| 3 |
=-
| 1 |
| 3 |
∴y=-
| 1 |
| 3 |
(3)解:如图,作A关于直线BC的对称点A′,连DA′交BC于Q,则这个点Q就是使△ADQ周长最小的点,

∵BQ∥AD,点B为AA′中点,
∴BQ为△A′AD的中位线,
此时Q是BC的中点,
最小周长为AD+A′D=3+
| AA′2+AD2 |
| 42+32 |
点评:本题主要考查了相似三角形的判定和性质、图形面积的求法、矩形的性质等知识.解题的关键是运用面积比等于相似比的平方.

练习册系列答案
相关题目
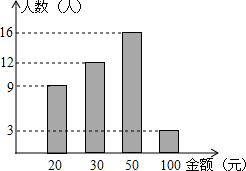 春节将至,某中学八年级(1)班共有40名同学参加了“春节送温暖”捐款活动.活动结束后,生活委员小林将捐款情况进行了统计,并绘制成如右的统计图.
春节将至,某中学八年级(1)班共有40名同学参加了“春节送温暖”捐款活动.活动结束后,生活委员小林将捐款情况进行了统计,并绘制成如右的统计图.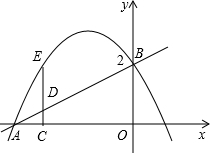 如图,在平面直角坐标系中,直线
如图,在平面直角坐标系中,直线 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是
如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是