题目内容
18.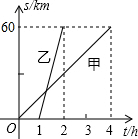 A、B两地相距60km,甲乙两人分别骑自行车和摩托车沿相同路线匀速行驶,由A地到达B地,他们行驶的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示
A、B两地相距60km,甲乙两人分别骑自行车和摩托车沿相同路线匀速行驶,由A地到达B地,他们行驶的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示(1)分别写出甲乙行驶的路程s(km)与甲出发后的时间t(h)之间的函数关系式;
(2)求出图象交点坐标,并解释交点的实际意义;
(3)直接写出在什么时间内乙在甲前;
(4)求出甲乙相距10km的时间;
(5)求出甲乙相距30km的时间.
分析 (1)根据待定系数法解出解析式即可;
(2)解方程组即可得到结论;
(3)根据交点坐标公式即可得到结论;
(4)根据题意列方程即可得到结论;
(5)根据题意列方程即可得到结论.
解答 解:(1)设甲的解析式为:s=kt,
把(4,60)代入解析式可得:k=15,
所以解析式为:s=15t;
设乙的解析式为:s=at+b,
把(1,0)和(2,60)代入解析式可得:$\left\{\begin{array}{l}{a+b=0}\\{2a+b=60}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=60}\\{b=-60}\end{array}\right.$,
故解析式为:s=60t-60;
(2)解$\left\{\begin{array}{l}{s=15t}\\{s=60t-60}\end{array}\right.$得$\left\{\begin{array}{l}{t=\frac{4}{3}}\\{s=20}\end{array}\right.$,
∴交点坐标为($\frac{4}{3}$,20),
∴交点的实际意义是甲出发后$\frac{4}{3}$小时时,甲与乙相遇;
(3)甲出发后$\frac{4}{3}$小时后,乙在甲前;
(4)①甲在乙前,即15t-60t+60=10,
∴t=$\frac{10}{9}$小时,
②乙在甲前,60t-60-15t=10,
∴t=$\frac{14}{9}$小时,
综上所述:当甲乙相距10km的时间是$\frac{10}{9}$小时或$\frac{14}{9}$小时;
(5)①甲在乙前,即15t-60t+60=30,
∴t=$\frac{2}{3}$小时,
②乙在甲前,60t-60-15t=30,
∴t=2小时,
综上所述:当甲乙相距30km的时间是$\frac{2}{3}$小时或2小时.
点评 本题考查了函数的图象,利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.

 全优点练单元计划系列答案
全优点练单元计划系列答案| A. | (2,3) | B. | (2,-3) | C. | (-2,3) | D. | (-2,-3) |
 如图,点A,B,C都在⊙O上,若∠OAC=17°,∠ACB=46°,AC与OB交于点D,则∠ODA的度数为71度.
如图,点A,B,C都在⊙O上,若∠OAC=17°,∠ACB=46°,AC与OB交于点D,则∠ODA的度数为71度.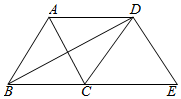 如图,△ABC是边长为2的等边三角形,将△ABC沿射线BC向右平移得到△DCE,连接AD、BD,则下列四个结论:AD∥BC、AC⊥BD、∠BDA=∠BDC、四边形ABED面积为4$\sqrt{3}$,其中错误的个数为( )
如图,△ABC是边长为2的等边三角形,将△ABC沿射线BC向右平移得到△DCE,连接AD、BD,则下列四个结论:AD∥BC、AC⊥BD、∠BDA=∠BDC、四边形ABED面积为4$\sqrt{3}$,其中错误的个数为( )