题目内容
15.已知二次函数y=-x2-4x+3,则2x+y的最大值是4.分析 先用x表示2x+y得到2x+y=2x-x2-4x+3,然后把解析式配成顶点式,然后根据二次函数的最值问题求解.
解答 解:2x+y=2x-x2-4x+3=-x2-2x+3=-(x+1)2+4,
所以x=-1时,2x+y的最大值为4.
故答案为4.
点评 本题考查了二次函数的最值:对于二次函数y=ax2+bx+c(a≠0),其顶点式为y=a(x+$\frac{b}{2a}$)2+$\frac{4ac-{b}^{2}}{4a}$当a>0时,抛物线在对称轴左侧,y随x的增大而减少;在对称轴右侧,y随x的增大而增大,因为图象有最低点,所以函数有最小值,当x=-$\frac{b}{2a}$时,y=$\frac{4ac-{b}^{2}}{4a}$;当a<0时,抛物线在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随x的增大而减少,因为图象有最高点,所以函数有最大值,当x=-$\frac{b}{2a}$时,y=$\frac{4ac-{b}^{2}}{4a}$.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
5.下列计算结果正确的是( )
| A. | m•m3=m4 | B. | 5a2-3a2=2 | C. | x3+x3=x6 | D. | b12÷b3=b4 |
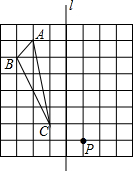 如图,△ABC是正方形网格上的格点三角形(顶点A、B、C在正方形网格的格点上)
如图,△ABC是正方形网格上的格点三角形(顶点A、B、C在正方形网格的格点上)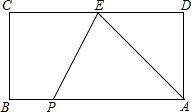 如图,长方形ABCD,AB=18,AD=8,E为CD边上一点,CE=12,
如图,长方形ABCD,AB=18,AD=8,E为CD边上一点,CE=12, △ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.作出△ABC关于y对称的△A1B1C1,并写出点△A1B1C1的坐标.
△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.作出△ABC关于y对称的△A1B1C1,并写出点△A1B1C1的坐标.