题目内容
6．
如图，在四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定四边形ABCD为平行四边形的是（ ）| A． | AB∥CD，AD∥BC | B． | OA=OC，OB=OD | C． | AB=CD，AD∥BC | D． | AB=CD，AD=BC |
分析 根据平行四边形的判定定理分别进行分析即可．
解答 解：A、根据两组对边分别平行的四边形是平行四边形可判定四边形ABCD为平行四边形，故此选项不合题意；
B、根据对角线互相平分的四边形是平行四边形可判定四边形ABCD为平行四边形，故此选项不合题意；
C、不能判定四边形ABCD是平行四边形，故此选项符合题意；
D、根据两组对边分别相等的四边形是平行四边形可判定四边形ABCD为平行四边形，故此选项不合题意；
故选：C．
点评 此题主要考查了平行四边形的判定，关键是掌握（1）两组对边分别平行的四边形是平行四边形．（2）两组对边分别相等的四边形是平行四边形．（3）一组对边平行且相等的四边形是平行四边形．（4）两组对角分别相等的四边形是平行四边形．（5）对角线互相平分的四边形是平行四边形．
练习册系列答案
相关题目
16．若a=-0.42，b=-4-2，c=（-$\frac{1}{4}$）-2，d=（-$\frac{1}{4}$）0，则a，b，c，d的大小关系是（ ）
| A． | a＜b＜d＜c | B． | b＜a＜d＜c | C． | a＜d＜c＜b | D． | c＜a＜d＜b |
17．下列方程中是一元一次方程的是（ ）
| A． | 2x-4=y+2 | B． | 5x-3=6x+1 | C． | xy=2 | D． | x+$\frac{1}{x}$=2 |
14．下列分式是最简分式的是（ ）
| A． | $\frac{2x}{{{x^2}+2}}$ | B． | $\frac{x-1}{{{x^2}-1}}$ | C． | $\frac{4}{2x}$ | D． | $\frac{1-x}{x-1}$ |
1．下列不等式变形正确的是（ ）
| A． | 如果a＞b，那么-3a＞-3b | B． | 如果2a＞-3，那么$a＜-\frac{3}{2}$ | ||
| C． | 如果-a＞-b，那么m-a＞m-b | D． | 如果$-\frac{1}{2}＞-1$，那么$-\frac{1}{2}a＞-a$ |
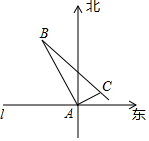如图，在东西方向的海岸线l上有一观察站A，某时刻测得一艘沿匀速直线航行的轮船位于观察站A的北偏西30°且与观察站A相距40km的B处，经过1h20min，又测得该轮船位于观察站A的北偏东60°且与观察站A相距8$\sqrt{3}$km的C处，在求该轮船航行的速度（结果保留根号）
18．
将一副三角板按图中方式叠放，则∠α等于（ ）
将一副三角板按图中方式叠放，则∠α等于（ ）| A． | 90° | B． | 75° | C． | 60° | D． | 45° |
15．下列各式中与a-b+c相等的是（ ）
| A． | a-（+b）-（+c） | B． | a-（+b）-（-c） | C． | a+（-b）+（-c） | D． | a+（-b）-（+c） |
如图是2002年8月在北京召开的国际数学家大会的会标，它取材于我国古代数学家赵爽的《勾股圆方图》，由四个全等的直角三角形和一个小正方形的拼成的大正方形，如果大正方形的面积是5，小正方形的面积是1，直角三角形的较短边为a，较长边为b，那么（a+b）2的值是（ ）