题目内容
11.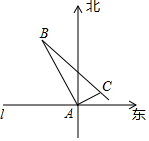 如图,在东西方向的海岸线l上有一观察站A,某时刻测得一艘沿匀速直线航行的轮船位于观察站A的北偏西30°且与观察站A相距40km的B处,经过1h20min,又测得该轮船位于观察站A的北偏东60°且与观察站A相距8$\sqrt{3}$km的C处,在求该轮船航行的速度(结果保留根号)
如图,在东西方向的海岸线l上有一观察站A,某时刻测得一艘沿匀速直线航行的轮船位于观察站A的北偏西30°且与观察站A相距40km的B处,经过1h20min,又测得该轮船位于观察站A的北偏东60°且与观察站A相距8$\sqrt{3}$km的C处,在求该轮船航行的速度(结果保留根号)
分析 根据∠1=30°,∠2=60°,可知△ABC为直角三角形.根据勾股定理解答.
解答  解:∵∠1=30°,∠2=60°,
解:∵∠1=30°,∠2=60°,
∴△ABC为直角三角形.
∵AB=40km,AC=8$\sqrt{3}$km,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{4{0}^{2}+(8\sqrt{3})^{2}}$=16$\sqrt{7}$(km).
∵1小时20分钟=80分钟,1小时=60分钟,
∴$\frac{16\sqrt{7}}{80}$×60=12$\sqrt{7}$(千米/小时).
点评 此题结合方向角,考查了阅读理解能力、解直角三角形的能力.利用勾股定理求得BC的长是解题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
1.下列说法正确的是( )
| A. | 单项式-2xy2的次数是2次 | B. | -2x2y与2xy2是同类项 | ||
| C. | $x+\frac{1}{x}+3$不是多项式 | D. | $\frac{{3a{b^3}}}{5}$的系数是3 |
6. 如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
 如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )| A. | AB∥CD,AD∥BC | B. | OA=OC,OB=OD | C. | AB=CD,AD∥BC | D. | AB=CD,AD=BC |
16.有一块多边形形状的草坪,在设计的图纸上,其中两条边的长度分别为5cm,6cm,经实地测量,5cm长的实际长度为15cm,则6cm长的边的实际长度为( )
| A. | 18m | B. | 16m | C. | 14m | D. | 12m |
1.下列各数2π,-5,0.$\stackrel{•}{4}$,-3.14,0中,负数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
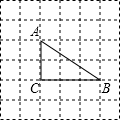 如图,在6×6的网格(小正方形的边长为1)中有一个△ABC,则AB边的长是$\sqrt{13}$,△ABC的周长是5+$\sqrt{13}$.
如图,在6×6的网格(小正方形的边长为1)中有一个△ABC,则AB边的长是$\sqrt{13}$,△ABC的周长是5+$\sqrt{13}$.