题目内容
3.顶点为(1,-3),且过点(0,-2)的抛物线相应的函数表达式为y=(x-1)2-3.分析 设抛物线的顶点式,将(0,-2)代入求得a的值即可得.
解答 解:根据题意设抛物线的解析式为y=a(x-1)2-3,
将(0,-2)代入可得,
a-3=-2,
解得:a=1,
∴解析式为y=(x-1)2-3,
故答案为:(x-1)2-3.
点评 本题主要考查待定系数法求函数解析式,在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
13.下列变形正确的是( )
| A. | 若2x+3=y-7,则2x+5=y-9 | B. | 若0.25x=-4,则x=-1 | ||
| C. | 若m-2=n+3,则m-n=2+3 | D. | 若-$\frac{1}{3}$y=-1,则y=-3 |
14. 如果小强将镖随意投中如图所示的正方形木板,那么镖落在阴影部分的概率为( )
如果小强将镖随意投中如图所示的正方形木板,那么镖落在阴影部分的概率为( )
 如果小强将镖随意投中如图所示的正方形木板,那么镖落在阴影部分的概率为( )
如果小强将镖随意投中如图所示的正方形木板,那么镖落在阴影部分的概率为( )| A. | $\frac{1}{9}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{6}$ |
18.正六边形的边长为2,则它的面积为( )
| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
8.若a>0且ax=2,ay=3,则ax-y的值为( )
| A. | 6 | B. | 5 | C. | -1 | D. | $\frac{2}{3}$ |
15.36的平方根是( )
| A. | ±6 | B. | ±18 | C. | 6 | D. | -6 |
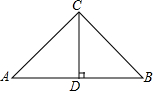 如图:在等腰直角△ABC中,CA=CB,CD⊥AB于D,AB=10,则CD=5.
如图:在等腰直角△ABC中,CA=CB,CD⊥AB于D,AB=10,则CD=5. 如图,△ABC中,∠A=25°,∠B=70°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,则∠EDF=22.5°.
如图,△ABC中,∠A=25°,∠B=70°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,则∠EDF=22.5°.