题目内容
17.已知△ABC中,AB=15,AC=13,AD⊥BC于D,AD=12,⊙O是△ABC的外接圆,则⊙O的半径是$\frac{65}{8}$.分析 分两种情形当△ABC是锐角三角形或钝角三角形,分别求解即可;
解答 解:当△ABC是锐角三角形时,如图,AE是△ABC外接圆的直径.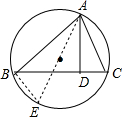
在Rt△ABD中,BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{1{5}^{2}-1{2}^{2}}$=9,
在Rt△ACD中,CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
∵∠C=∠E,∠ADC=∠ABE=90°,
∴△ADC∽△ABE,
∴$\frac{AD}{AB}$=$\frac{AC}{AE}$,
∴$\frac{12}{15}$=$\frac{13}{AE}$,
∴AE=$\frac{65}{4}$,
∴△ABC的外接圆的半径为$\frac{65}{8}$.
当△ABC是钝角三角形时,如图,CE是△ABC的外接圆的直径,作CF⊥AB于F.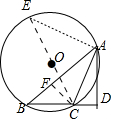
∵$\frac{1}{2}$•AB•CF=$\frac{1}{2}$•BC•AD,
可得CF=$\frac{16}{5}$,
由△AEC∽△FBC,可得$\frac{AC}{CF}$=$\frac{CE}{CB}$,
∴$\frac{13}{\frac{16}{5}}$=$\frac{CE}{4}$,
∴CE=$\frac{65}{4}$,
∴△ABC的外接圆的半径为$\frac{65}{8}$,
综上所述,△ABC的外接圆的半径为$\frac{65}{8}$.
故答案为$\frac{65}{8}$.
点评 本题考查了三角形的外接圆和外心,相似三角形的性质和判定,勾股定理,作出辅助线构建直角三角形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.某校数学兴趣小组经过市场调查,得到某品牌书包每月的销量与售价的相关信息如下表:
已知该品牌书包的进价为每个70元,若设售价为每个x元,月销量为y件.
(1)求y与x的关系式;
(2)已知每个书包的利润不低于10元且不超过100元,问售价为多少元时,当月的销量最大,最大销量是多少?
| 售价(元/个) | 100 | 110 | 120 | 130 | … |
| 月销量(个) | 200 | 180 | 160 | 140 | … |
(1)求y与x的关系式;
(2)已知每个书包的利润不低于10元且不超过100元,问售价为多少元时,当月的销量最大,最大销量是多少?
12.下列运算正确的是( )
| A. | 2a3÷a=6 | B. | (a+b)(a-b)=a2-b2 | C. | (ab3)2=a2b5 | D. | (a+b)2=a2+b2 |
9.下列计算正确的是( )
| A. | (a2b)3=a6b3 | B. | a3•a2=a4 | C. | b4+b4=2b8 | D. | (a-b)(b-a)=a2-b2 |