题目内容
18.用适当的方法解下列方程:(1)(2x+1)2-5=0
(2)-x2-4$\sqrt{2}$x+10=0
(3)2(2x-3)2-3(2x-3)=0.
分析 (1)利用直接开方法解即可.
(2)利用因式分解解比较简单.
(3)提公因式法,用因式分解法解即可.
解答 解:(1)∵(2x+1)2=5,
∴2x+1=$±\sqrt{5}$,
∴x1=$\frac{-1+\sqrt{5}}{2}$,x2=$\frac{-1-\sqrt{5}}{2}$.
(2)∵x2+4$\sqrt{2}$x-10=0,
∴(x+5$\sqrt{2}$)(x-$\sqrt{2}$)=0,
∴x1=-5$\sqrt{2}$,x2=$\sqrt{2}$.
(3)∵2(2x-3)2-3(2x-3)=0.
∴(2x-3)(4x-6-3)=0,
∴(2x-3)(4x-9)=0,
∴x1=$\frac{3}{2}$,x2=$\frac{9}{4}$.
点评 本题考查一元二次方程的解法,解题的关键是灵活掌握一元二次方程的解法,一元二次方程的解法有直接开方法,因式分解法,公式法,配方法,属于中考常考题型.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
9.已知一个三角形的两边长分别为3和6,第三边的长是方程(x-2)(x-4)=0的根,则这个三角形的周长为( )
| A. | 13 | B. | 11 | C. | 13或11 | D. | 15 |
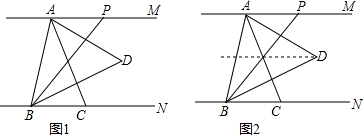
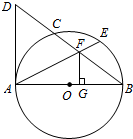 如图,AB是⊙O的直径,BD交⊙O于点C,E为 BC 的中点,连接AE交BD于点F,作FG⊥AB,垂足为G,连接AD,且∠D=2∠BAE.
如图,AB是⊙O的直径,BD交⊙O于点C,E为 BC 的中点,连接AE交BD于点F,作FG⊥AB,垂足为G,连接AD,且∠D=2∠BAE. 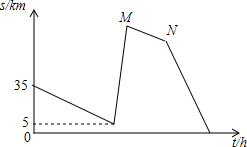 甲、乙两车准备从A地开往B地,由于甲车比乙车慢,所以甲车先出发半小时后乙车再追赶甲车,当乙车出发3h到达一丁字路口时,改变了行进方向,行进了40km后发现选错了行进方向,于是立即调转车头按原速继续追赶甲车,当乙车又追赶了1h后,甲车到达了B地,再行进过程中两车都保持匀速.甲、乙两车间的路程s(单位:km)与乙车行驶的时间t(单位:h)之间的函数图象如图所示,请根据图象信息解答下列问题:
甲、乙两车准备从A地开往B地,由于甲车比乙车慢,所以甲车先出发半小时后乙车再追赶甲车,当乙车出发3h到达一丁字路口时,改变了行进方向,行进了40km后发现选错了行进方向,于是立即调转车头按原速继续追赶甲车,当乙车又追赶了1h后,甲车到达了B地,再行进过程中两车都保持匀速.甲、乙两车间的路程s(单位:km)与乙车行驶的时间t(单位:h)之间的函数图象如图所示,请根据图象信息解答下列问题: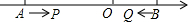 如图,数轴上的点A,B对应的数分别为-10,5.动点P,Q分别从A,B同时出发,点P以每秒3个单位长度的速度沿数轴向右匀速运动,点Q以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
如图,数轴上的点A,B对应的数分别为-10,5.动点P,Q分别从A,B同时出发,点P以每秒3个单位长度的速度沿数轴向右匀速运动,点Q以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.