题目内容
5.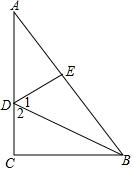 △ABC中,∠C=90°,点D、E分别为AC、AB上点,AD=BD,AE=BC,DE=DC,求证:∠1=∠2.
△ABC中,∠C=90°,点D、E分别为AC、AB上点,AD=BD,AE=BC,DE=DC,求证:∠1=∠2.
分析 根据全等三角形的判定定理SSS推知△ADE≌△BDC,则该全等三角形的对应角相等:∠AED=∠C=90°,故∠DEB=90°,然后由全等直角三角形的判定定理Rt△BCD≌Rt△BED,故对应角相等,证得结论.
解答 证明:∵在△ADE与△BDC中,$\left\{\begin{array}{l}{AD=BD}\\{AE=BC}\\{DE=DC}\end{array}\right.$,
∴△ADE≌△BDC(SSS),
∴∠AED=∠C=90°,故∠DEB=90°.
∴在Rt△BCD与Rt△BED中,$\left\{\begin{array}{l}{DC=DE}\\{BD=BD}\end{array}\right.$,
∴Rt△BCD≌Rt△BED(HL),
∴∠1=∠2.
点评 本题考查了全等三角形的判定与性质.注意:全等三角形的判定、全等三角形的性质的综合应用.

练习册系列答案
相关题目
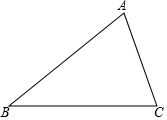 尺规作图:如图,已知△ABC,求作△A1B1C1,使A1B1=AB,∠B1=∠B,B1C1=BC.(作图要求:写已知、求作,不写作法,保留作图痕迹)
尺规作图:如图,已知△ABC,求作△A1B1C1,使A1B1=AB,∠B1=∠B,B1C1=BC.(作图要求:写已知、求作,不写作法,保留作图痕迹)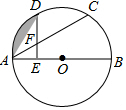 如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE⊥AB,垂足为E,DE交AC于点F.
如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE⊥AB,垂足为E,DE交AC于点F.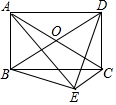 如图,在?ABCD中,对角线AC,BD相交于点O,E是?ABCD外一点,且∠AEC=∠BED=90°,求证:?ABCD是矩形.
如图,在?ABCD中,对角线AC,BD相交于点O,E是?ABCD外一点,且∠AEC=∠BED=90°,求证:?ABCD是矩形.