题目内容
13.求证:无论x取任何实数,代数式x2+8x+18的值总大于0(提示:用配方法配成(x+a)2+k的形式)分析 先把原式配方得到(x+a)2+k,然后根据非负数的性质进行证明.
解答 证明:x2+8x+18
=(x2+8x+16-16)+18,
=(x+4)2+2,
∵(x+4)2≥0,
∴(x+4)2+2>0,
即无论x取什么实数,代数式x2+8x+18的值总大于0.
点评 本题考查了配方法的应用:配方法的理论依据是公式a2±2ab+b2=(a±b)2.二次三项式是完全平方式,则常数项是一次项系数一半的平方.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
15.下列各式属于最简二次根式的是( )
| A. | $\sqrt{0.1}$ | B. | $\sqrt{8}$ | C. | $\sqrt{{x^2}+{x^2}y}$ | D. | $\sqrt{{x^2}+1}$ |
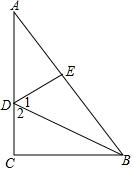 △ABC中,∠C=90°,点D、E分别为AC、AB上点,AD=BD,AE=BC,DE=DC,求证:∠1=∠2.
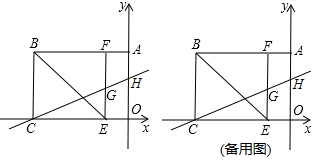
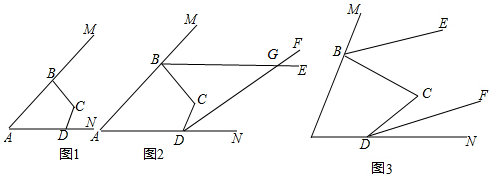
△ABC中,∠C=90°,点D、E分别为AC、AB上点,AD=BD,AE=BC,DE=DC,求证:∠1=∠2. 如图,求∠A+∠B+∠C+∠D+∠E+∠F的值.
如图,求∠A+∠B+∠C+∠D+∠E+∠F的值.