题目内容
11.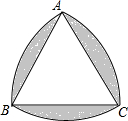 如图,△ABC是等边三角形,AB=2,分别以A,B,C为圆心,以2为半径作弧,则图中阴影部分的面积是2π-3$\sqrt{3}$.
如图,△ABC是等边三角形,AB=2,分别以A,B,C为圆心,以2为半径作弧,则图中阴影部分的面积是2π-3$\sqrt{3}$.
分析 根据等边三角形的面积公式求出正△ABC的面积,根据扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$求出扇形的面积,求差得到答案.
解答 解:∵正△ABC的边长为2,
∴△ABC的面积为$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
扇形ABC的面积为$\frac{60•π×{2}^{2}}{360}$=$\frac{2}{3}$π,
则图中阴影部分的面积=3×($\frac{2}{3}$π-$\sqrt{3}$)=2π-3$\sqrt{3}$,
故答案为:2π-3$\sqrt{3}$.
点评 本题考查的是等边三角形的性质和扇形的面积计算,掌握扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$是解题的关键.

练习册系列答案
相关题目
1. 如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )
如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )
 如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )
如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
2.下列计算正确的是( )
| A. | a3+a3=a6 | B. | 3a-a=3 | C. | (a3)2=a5 | D. | a•a2=a3 |
19.-12等于( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
6.抛物线y=2x2-2$\sqrt{2}$x+1与坐标轴的交点个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.