题目内容
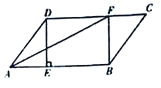
【题目】如图,![]() 于
于![]() ,以
,以![]() 直径作
直径作![]() ,交
,交![]() 于点
于点![]() 恰有
恰有![]() ,连接
,连接![]() .
.
(1)如图1,求证:![]() ;
;
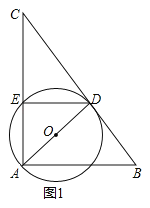
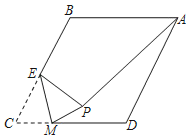
(2)如图2,连接![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() 连接
连接![]() 试探究
试探究![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;

(3)在(2)的基础上,若![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() ;理由见解析;(3)
;理由见解析;(3)![]() .
.
【解析】
(1)由直径所对圆周角等于90度可得![]() ,进而易证
,进而易证![]() ,再根据
,再根据![]() 即可证明
即可证明![]() ;
;
(2)由![]() ,可得
,可得![]() ,进而可知
,进而可知![]() ,再由同弧所对圆周角相等可得
,再由同弧所对圆周角相等可得![]() ,再分别证明
,再分别证明![]() ,
, ![]() ,从而可得
,从而可得![]() ,即可解决问题;
,即可解决问题;
(3)设![]() ,
,![]() ,由
,由![]() ,可得
,可得![]() ,可得
,可得![]() ,由
,由![]() ,可得
,可得![]() ,设
,设![]() ,
,![]() ,根据
,根据![]() ,可得
,可得![]() ,求出
,求出![]() 即可解决问题.
即可解决问题.
解:(1)证明: ![]() 是直径,
是直径,
![]()
![]() ,
,
∵![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又∵![]() ,
,
![]() (AAS).
(AAS).
(2)结论:![]() .理由如下:
.理由如下:
由(1)可得:![]() ,
,
![]() ,
,
![]() ,
,
![]() 是直径,
是直径,
![]()
∴![]() ,
,
![]() ,
,
![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(3)解:设![]() ,
,![]() ,
,

![]() ,
,
![]()
![]() ,
,
![]()
![]()
整理得![]() ,
,
![]() 或
或![]() (舍弃),
(舍弃),
![]() ,
,
![]()
![]() ,
,
又∵由(2)可知![]() ,
,
![]()
![]() ,
,
![]() ,
,
∵![]() ,
,![]()
∴![]() ,
,
∴![]() ,
,
设![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目