ЬтФПФкШн
ЁОЬтФПЁПЮвУЧЖЈвхЃКАб![]() НазіКЏЪ§
НазіКЏЪ§![]() ЕФАщЫцКЏЪ§ЃЎБШШчЃК
ЕФАщЫцКЏЪ§ЃЎБШШчЃК![]() ОЭЪЧ
ОЭЪЧ![]() ЕФАщЫцКЏЪ§ЃЎЪ§аЮНсКЯЪЧбЇЯАКЏЪ§ЕФвЛжжживЊЗНЗЈЃЌЖдгкЖўДЮКЏЪ§
ЕФАщЫцКЏЪ§ЃЎЪ§аЮНсКЯЪЧбЇЯАКЏЪ§ЕФвЛжжживЊЗНЗЈЃЌЖдгкЖўДЮКЏЪ§![]() ЃЈ
ЃЈ![]() ЕФГЃЪ§ЃЉЃЌШєЕу
ЕФГЃЪ§ЃЉЃЌШєЕу![]() дкКЏЪ§
дкКЏЪ§![]() ЕФЭМЯёЩЯЃЌдђЕуЃЈ
ЕФЭМЯёЩЯЃЌдђЕуЃЈ![]() ЃЌ
ЃЌ![]() ЃЉвВдкЦфЭМЯёЩЯЃЌМДДгЪ§ЕФНЧЖШПЩвджЊЕРЫќЕФЭМЯёЙигк
ЃЉвВдкЦфЭМЯёЩЯЃЌМДДгЪ§ЕФНЧЖШПЩвджЊЕРЫќЕФЭМЯёЙигк![]() жсЖдГЦЃЎНтД№ЯТСаЮЪЬтЃК
жсЖдГЦЃЎНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉ![]() ЕФЭМЯёЙигк жсЖдГЦЃЛ
ЕФЭМЯёЙигк жсЖдГЦЃЛ
ЃЈ2ЃЉЂйжБНгаДГіКЏЪ§![]() ЕФАщЫцКЏЪ§ЕФБэДяЪН ЃЛ
ЕФАщЫцКЏЪ§ЕФБэДяЪН ЃЛ
ЂкдкШчЭМЂйЫљЪОЕФЦНУцжБНЧзјБъЯЕжаЛГі![]() ЕФАщЫцКЏЪ§ЕФДѓжТЭМЯёЃЛ
ЕФАщЫцКЏЪ§ЕФДѓжТЭМЯёЃЛ
ЃЈ3ЃЉШєжБЯп![]() гы
гы![]() ЕФАщЫцКЏЪ§ЭМЯёНЛгк
ЕФАщЫцКЏЪ§ЭМЯёНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЈЕуAдкЕуBЕФЩЯЗНЃЉЃЌСЌНг
СНЕуЃЈЕуAдкЕуBЕФЩЯЗНЃЉЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌЧвЁїABOЕФУцЛ§ЮЊ12ЃЌЧѓ
ЃЌЧвЁїABOЕФУцЛ§ЮЊ12ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ4ЃЉШєжБЯп![]() ЃЈ
ЃЈ![]() ВЛЦНаагкyжсЃЉгы
ВЛЦНаагкyжсЃЉгы![]() ЃЈ
ЃЈ![]() ЕФГЃЪ§ЃЉЕФАщЫцКЏЪ§ЭМЯёНЛгк
ЕФГЃЪ§ЃЉЕФАщЫцКЏЪ§ЭМЯёНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЈЕу
СНЕуЃЈЕу![]() ЁЂ
ЁЂ![]() ЗжБ№дкЕквЛЁЂЫФЯѓЯоЃЉЃЌЧв
ЗжБ№дкЕквЛЁЂЫФЯѓЯоЃЉЃЌЧв![]() ЃЌЪдЮЪ
ЃЌЪдЮЪ![]() ЁЂ
ЁЂ![]() СНЕуЕФзнзјБъЕФЛ§ЪЧЗёЮЊГЃЪ§ЃПШчЙћЪЧЃЌЧыИјгшжЄУїЃЛШчЙћВЛЪЧЃЌЧыЫЕУїРэгЩЃЎ
СНЕуЕФзнзјБъЕФЛ§ЪЧЗёЮЊГЃЪ§ЃПШчЙћЪЧЃЌЧыИјгшжЄУїЃЛШчЙћВЛЪЧЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЙигк![]() жсЖдГЦЃЛЃЈ2ЃЉЂй
жсЖдГЦЃЛЃЈ2ЃЉЂй![]() ЃЛЂкЯъМћНтЮіЃЛЃЈ3ЃЉ
ЃЛЂкЯъМћНтЮіЃЛЃЈ3ЃЉ![]() ЃЛЃЈ4ЃЉ
ЃЛЃЈ4ЃЉ![]() ЁЂ
ЁЂ![]() СНЕуЕФзнзјБъжЎЛ§ЮЊГЃЪ§ЃЌРэгЩМћЯъНтЃЎ
СНЕуЕФзнзјБъжЎЛ§ЮЊГЃЪ§ЃЌРэгЩМћЯъНтЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОн![]() ЬиЕуЃЌМДПЩЧѓГі
ЬиЕуЃЌМДПЩЧѓГі![]() ЕФЭМЯёЙигк
ЕФЭМЯёЙигк![]() жсЖдГЦЃЛ
жсЖдГЦЃЛ
ЃЈ2ЃЉИљОнАщЫцКЏЪ§ЕФЖЈвхЃЌПЩвдаДГіД№АИЃЛ
ЃЈ3ЃЉЯШЧѓГіжБЯп![]() гы
гы![]() жсгкЕу
жсгкЕу![]() ЃЌНтЗНГЬзщ
ЃЌНтЗНГЬзщ![]() ЃЌгУКЌkЕФЪНзгБэЪОy1,y2ЃЌНјЖјБэЪОГі
ЃЌгУКЌkЕФЪНзгБэЪОy1,y2ЃЌНјЖјБэЪОГі![]() ЃЌИљОнЁїABOЕФУцЛ§ЮЊ12ЃЌЧѓГі
ЃЌИљОнЁїABOЕФУцЛ§ЮЊ12ЃЌЧѓГі![]() ЃЌМДПЩЧѓГіkЃЛ
ЃЌМДПЩЧѓГіkЃЛ
ЃЈ4ЃЉЩш![]() ЁЂ
ЁЂ![]() ЃЌЗжБ№Й§
ЃЌЗжБ№Й§![]() зї
зї![]() жсЃЌ
жсЃЌ![]() жсЃЌДЙзуЗжБ№ЮЊ
жсЃЌДЙзуЗжБ№ЮЊ![]() ЃЌПЩжЄЕУ
ЃЌПЩжЄЕУ![]() ЃЌ
ЃЌ![]() ЃЌгУAЁЂBЕФзјБъБэЪОГіРДЃЌНсКЯ
ЃЌгУAЁЂBЕФзјБъБэЪОГіРДЃЌНсКЯ![]() ЕФАщЫцКЏЪ§ЙиЯЕЪНЃЌЕУЕН
ЕФАщЫцКЏЪ§ЙиЯЕЪНЃЌЕУЕН![]() ЁЂ
ЁЂ![]() СНЕуЕФзнзјБъЕФЛ§ЮЊ
СНЕуЕФзнзјБъЕФЛ§ЮЊ![]() ЃЌЮЪЬтЕУНтЃЎ
ЃЌЮЪЬтЕУНтЃЎ
НтЃКЃЈ1Щш![]() дк
дк![]() ЕФЭМЯёЩЯЃЌдђ
ЕФЭМЯёЩЯЃЌдђ![]()
![]() КЏЪ§ЭМЯёЩЯЃЌЫљвд
КЏЪ§ЭМЯёЩЯЃЌЫљвд![]() ЕФЭМЯёЙигк Йигк
ЕФЭМЯёЙигк Йигк![]() жсЖдГЦЃЛ
жсЖдГЦЃЛ
ЃЈ2ЃЉЂй![]() ЂкЭМЯёШчЭМЃК
ЂкЭМЯёШчЭМЃК
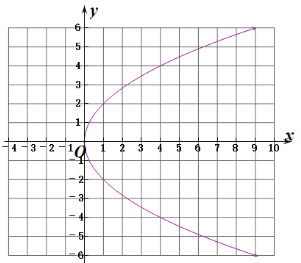
ЃЈ3ЃЉЁп![]() ЁрЕБ
ЁрЕБ![]() ЪБ
ЪБ![]() ЃЌ
ЃЌ
ЁржБЯпНЛ![]() жсгкЕу
жсгкЕу![]() Ёр
Ёр![]()
Щш![]() ЃЌ
ЃЌ![]() ЃЌОнЬтвтга
ЃЌОнЬтвтга![]()
Ёр![]() Ёр
Ёр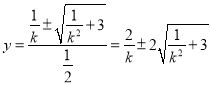
Ёр![]() гжЁп
гжЁп![]()
Ёр![]()
Ёр![]() Ёр
Ёр![]()
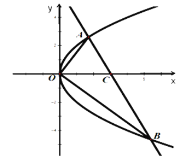
ЃЈ4ЃЉ![]() ЁЂ
ЁЂ![]() СНЕуЕФзнзјБъжЎЛ§ЮЊГЃЪ§
СНЕуЕФзнзјБъжЎЛ§ЮЊГЃЪ§
ЁпЕу![]() Ољдк
Ољдк![]() ЭМЯёЩЯЃЌЧв
ЭМЯёЩЯЃЌЧв![]() ЁЂ
ЁЂ![]() ЗжБ№дкЕквЛЁЂЫФЯѓЯо
ЗжБ№дкЕквЛЁЂЫФЯѓЯо
ЁрПЩЩш![]() ЁЂ
ЁЂ![]()
ЗжБ№Й§![]() зї
зї![]() жсЃЌ
жсЃЌ![]() жсЃЌДЙзуЗжБ№ЮЊ
жсЃЌДЙзуЗжБ№ЮЊ![]()
гжЁп![]() Ёр
Ёр![]()
Ёр![]() Ёр
Ёр![]()
Ёр![]() Ёр
Ёр![]()
Ёр![]()
Ёп![]() ЮЊГЃЪ§Ёр
ЮЊГЃЪ§Ёр![]() СНЕуЕФзнзјБъжЎЛ§ЮЊГЃЪ§ЃЎ
СНЕуЕФзнзјБъжЎЛ§ЮЊГЃЪ§ЃЎ
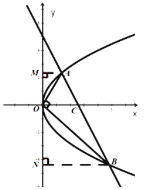

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПФГЭЌбЇдкРћгУУшЕуЗЈЛЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЃН0ЃЉЕФЭМЯѓЪБЃЌЯШШЁздБфСПxЕФвЛаЉжЕЃЌМЦЫуГіЯргІЕФКЏЪ§жЕyЃЌШчЯТБэЫљЪОЃК
x | Ё | 0 | 1 | 2 | 3 | 4 | Ё |
y | Ё | Љ3 | 0 | Љ1 | 0 | 3 | Ё |
НгзХЃЌЫћдкУшЕуЪБЗЂЯжЃЌБэИёжагавЛзщЪ§ОнМЦЫуДэЮѓЃЌЫћМЦЫуДэЮѓЕФвЛзщЪ§ОнЪЧЃЈЁЁЁЁЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()