题目内容
9.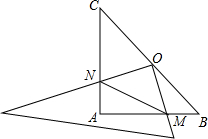 在你身边45°角的三角板ABC中,AB=AC,∠BAC=90°,O为BC的中点,
在你身边45°角的三角板ABC中,AB=AC,∠BAC=90°,O为BC的中点,(1)试问点O到△ABC的三个顶点A、B、C的距离有何关系,说明理由.
(2)如果将你身边另一块三角板的直角顶点放在O点上,两条直角边分别与AC、AB相交于N、M,请你探索说明△OMN的形状,并证明你的结论.
分析 (1)连接OA,得出△ABO和△ACO都是等腰直角三角形,得出0A=0B=OC,据此即可解答;
(2)△OMN的为等腰直角三角形,证明△ONA≌△OMB,得到ON=OM,又∠NOM直角,所以△OMN的为等腰直角三角形.
解答 解:(1)点O到△ABC的三个顶点A、B、C的距离相等,
如图,连接OA,
∵AB=AC,∠BAC=90°,O为BC的中点,
∴△ABO和△ACO都是等腰直角三角形,
∴0A=0B=OC,
∴点O到△ABC得三个顶点A、B、C的距离相等;
(2)△OMN的形状为等腰直角三角形.
∵AB=AC,∠BAC=90°,O为BC的中点,
∴∠AOB=90°,∠CAO=∠BAO=45°,∠ABO=45°,
∵∠MON=90°,
∴∠AON+∠AOM=90°,
∵∠BOM+∠AOM=90°,
∴∠AON=∠BOM,
在△ONA和△OMB中,
$\left\{\begin{array}{l}{∠AON=∠BOM}\\{AO=BO}\\{∠NAO=∠MBO}\end{array}\right.$
∴△ONA≌△OMB,
∴ON=OM,
又∵∠NOM直角,
∴△OMN的为等腰直角三角形.
点评 本题主要考查了等腰直角三角形的性质、全等三角形的判定和性质,在(2)中的关键是证明△ONA≌△OMB.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.解分式方程$\frac{1-x}{x-2}+2=\frac{1}{2-x}$的结果是( )
| A. | x=2 | B. | x=3 | C. | x=4 | D. | 无解 |
4.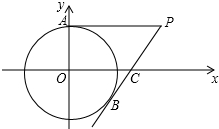 如图,在平面直角坐标系中.以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切与点B,交PB与⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C,则BC的长是( )
如图,在平面直角坐标系中.以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切与点B,交PB与⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C,则BC的长是( )
 如图,在平面直角坐标系中.以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切与点B,交PB与⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C,则BC的长是( )
如图,在平面直角坐标系中.以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切与点B,交PB与⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C,则BC的长是( )| A. | $\frac{5}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{2}$ |
14. 如图,在△ABC中,AB=AC,P为△ABC的中线AD上任意一点,若点P到边AB的距离为2cm,则点P到边AC的距离为( )
如图,在△ABC中,AB=AC,P为△ABC的中线AD上任意一点,若点P到边AB的距离为2cm,则点P到边AC的距离为( )
 如图,在△ABC中,AB=AC,P为△ABC的中线AD上任意一点,若点P到边AB的距离为2cm,则点P到边AC的距离为( )
如图,在△ABC中,AB=AC,P为△ABC的中线AD上任意一点,若点P到边AB的距离为2cm,则点P到边AC的距离为( )| A. | 1cm | B. | 1.5cm | C. | 2cm | D. | 2.5cm |
1.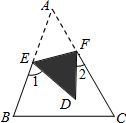 如图,△ABC中,∠A=50°,点E、F在AB、AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于( )
如图,△ABC中,∠A=50°,点E、F在AB、AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于( )
 如图,△ABC中,∠A=50°,点E、F在AB、AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于( )
如图,△ABC中,∠A=50°,点E、F在AB、AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于( )| A. | 130° | B. | 120° | C. | 65° | D. | 100° |
18.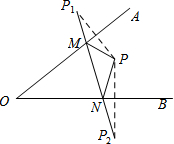 如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( )
如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( )
 如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( )
如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |