题目内容
19.计算:$\sqrt{3}$(2+$\sqrt{3}$)-$\sqrt{12}$.分析 先进行二次根式的乘法运算,然后化简后合并即可.
解答 解:原式=2$\sqrt{3}$+3-2$\sqrt{3}$
=3.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
10.在下列各数中是无理数的有( )
-0.333…,$\sqrt{4}$,-3π,$\sqrt{5}$,$\sqrt{9}$,3.1415926,2.010101…(相邻两个1之间有1个0),76.0123456…(小数部分由相继的正整数组成).
-0.333…,$\sqrt{4}$,-3π,$\sqrt{5}$,$\sqrt{9}$,3.1415926,2.010101…(相邻两个1之间有1个0),76.0123456…(小数部分由相继的正整数组成).
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
14.若$\frac{b}{a}=\frac{2}{3}$,则$\frac{a-b}{a}$的值是( )
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{5}$ |
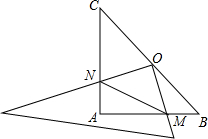 在你身边45°角的三角板ABC中,AB=AC,∠BAC=90°,O为BC的中点,
在你身边45°角的三角板ABC中,AB=AC,∠BAC=90°,O为BC的中点,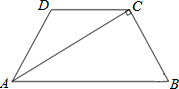 如图,在梯形ABCD中,AB∥DC,AD=BC,∠D=120°,AC⊥BC,求tan∠DAC的值.
如图,在梯形ABCD中,AB∥DC,AD=BC,∠D=120°,AC⊥BC,求tan∠DAC的值.
 如图,△ABD、△ACE都是正三角形,BE和CD交于O点,则DC=BE.(写等于哪条线段)
如图,△ABD、△ACE都是正三角形,BE和CD交于O点,则DC=BE.(写等于哪条线段)