题目内容
18.(1)计算:$\sqrt{27}$-|-$\sqrt{3}}$|+(-$\frac{1}{2}}$)-1-2sin60°(2)解方程$\frac{3}{2x-4}$-$\frac{x}{x-2}$=$\frac{1}{2}$.
分析 (1)原式利用二次根式性质,绝对值的代数意义,负整数指数幂法则,以及特殊角的三角函数值计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=3$\sqrt{3}$-$\sqrt{3}$-2-$\sqrt{3}$=$\sqrt{3}$-2;
(2)去分母得:3-2x=x-2,
解得:x=$\frac{5}{3}$,
经检验x=$\frac{5}{3}$是分式方程的解.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
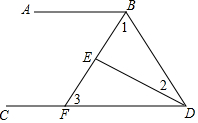 如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.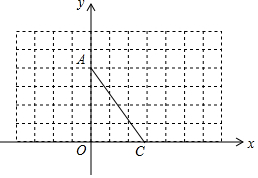 如图,在直角坐标系中,A(0,4),C(3,0).
如图,在直角坐标系中,A(0,4),C(3,0).