题目内容
7.已知函数y=(2m+1)x+m-3(1)若函数图象经过原点,求m的值;
(2)若函数的图象平行于直线y=3x-3,求m的值
(3)若这个函数是一次函数,且y随着x的增大而增大,且不经过第二象限,求m的取值范围.
分析 (1)根据已知条件知,关于x的一次函数y=2x+m-1的图象经过点(0,0),所以把(0,0)代入已知函数解析式列出关于系数m的方程,通过解方程即可求得m的值;
(2)函数的图象平行于直线y=3x-3,说明2m+1=3,由此求得m的数值即可;
(3)根据题意列不等式组即可得到结论.
解答 解:(1)∵关于x的一次函数y=(2m+1)x+m-3的图象经过原点,
∴点(0,0)满足一次函数的解析式y=(2m+1)x+m-3,
∴0=m-3,
解得m=3.
(2)∵函数y=(2m+1)x+m-3的图象平行于直线y=3x-3,
∴2m+1=3,
∴m=1;
(3)函数y=(2m+1)x+m-3是一次函数,且y随着x的增大而增大,且不经过第二象限,求m的取值范围.
∴2m+1>0且m-3≤0,
∴-$\frac{1}{2}<$m≤3,
∴m的取值范围是-$\frac{1}{2}<$m≤3.
点评 本题考查的是一次函数图象上点的坐标特点与两条直线平行的条件,熟知一次函数图象上各点一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
2.已知:12.52=156.25,12.62=158.76,12.72=161.29,12.82=163.84,下列说法正确的是( )
| A. | 12.6<$\sqrt{160}$<12.7 | B. | $\sqrt{160}$=40 | C. | 12.5<$\sqrt{156}$<12.6 | D. | $\sqrt{158.76}$=±12.6 |
19.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{13}$ | B. | $\sqrt{20}$ | C. | $\sqrt{8}$ | D. | $\frac{1}{\sqrt{2}}$ |
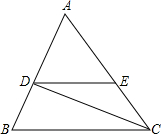 如图,CD是∠ACB的平分线,∠EDC=25°,∠DCE=25°,∠B=70°.
如图,CD是∠ACB的平分线,∠EDC=25°,∠DCE=25°,∠B=70°.